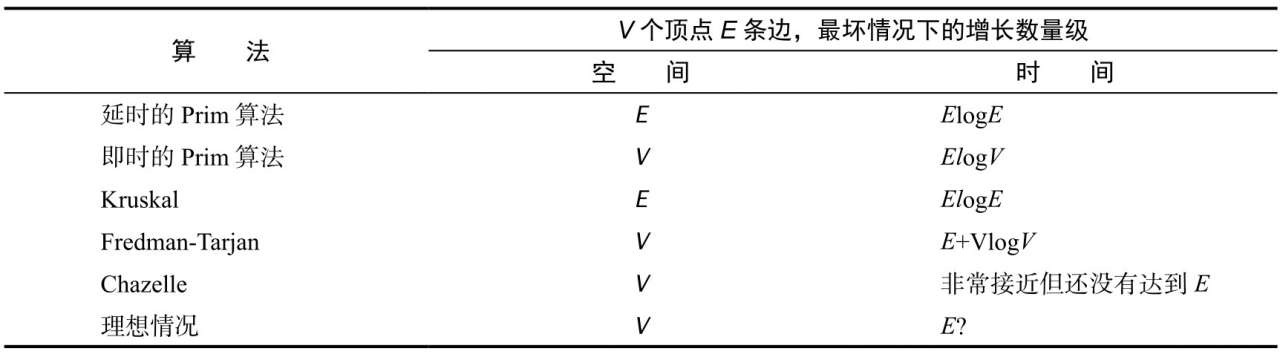
加权图（最小生成树）

加权图是一种为每条边关联一个权值或是成本的图模型。

这种图能够自然地表示许多应用。在一幅航空图中，边表示航线，权值则可以表示距离或是费用。在一幅电路图中，边表示导线，权值则可能表示导线的长度即成本，或是信号通过这条线路所需的时间。

图的生成树：是它的一棵含有其所有顶点的无环连通子图。
一幅加权图的最小生成树（MST）：是它的一棵权值（树中所有边的权值之和）最小的生成树。

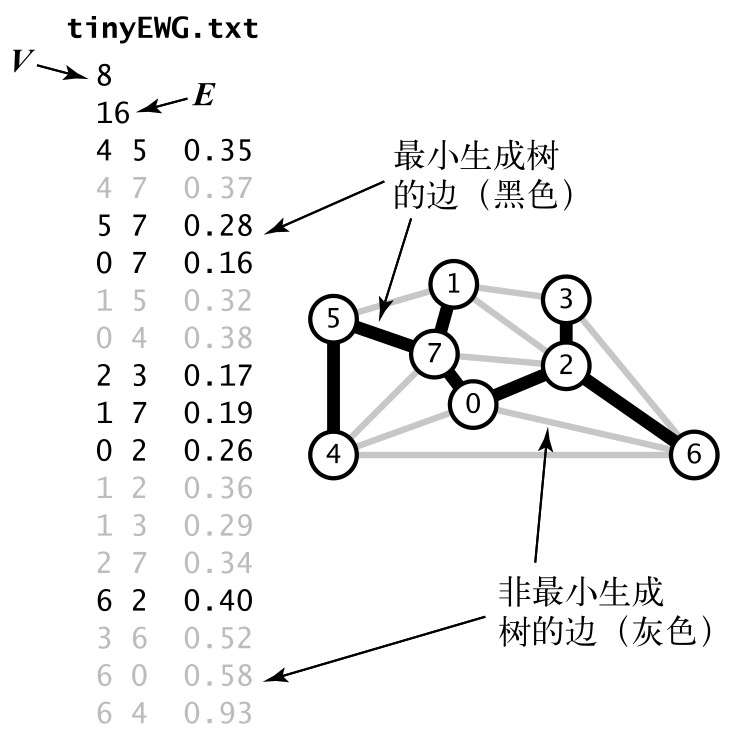
计算最小生成树的约定：

只考虑连通图
边的权重不一定表示距离
边的权重可能是 0 ，也可能是负数
所有边的权重各不相同。（如果有相同，那么最小生成树就不唯一了）

加权图的表示

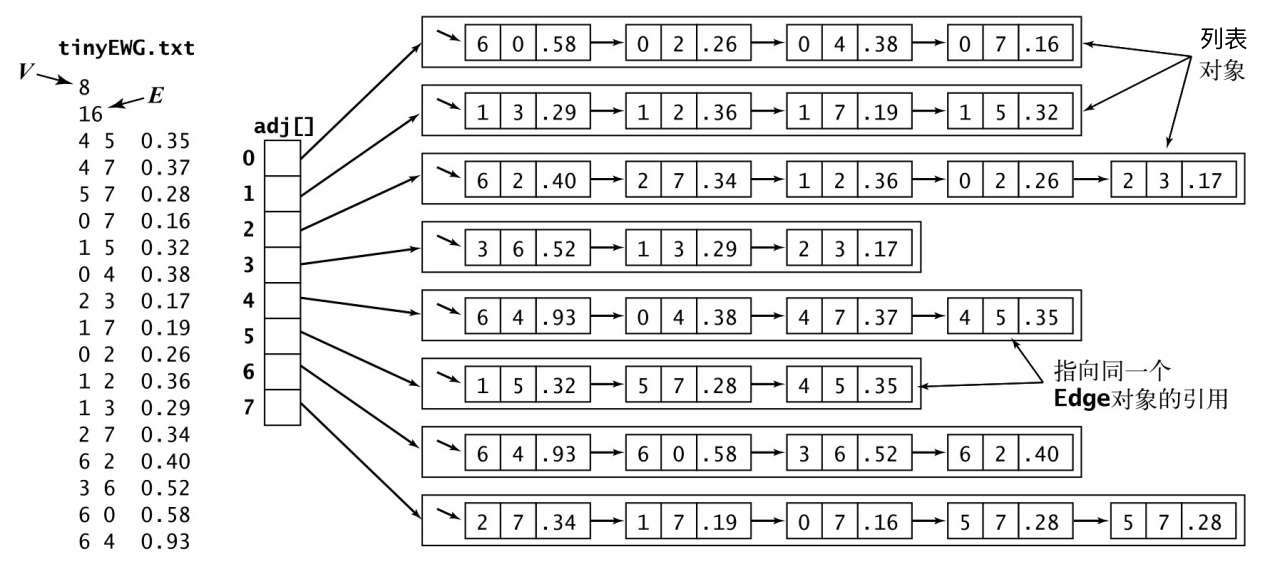
定义：

interface Edge {
  /** 边的权重 */
  weight: number
  /** 边两端一个顶点 */
  either: number
  /** 另一个顶点 */
  other: number
  /** 与另一条边比较 */
  compareTo: (that: Edge) => number
}

interface EdgeWeightedGraph extends Omit<Graph, 'adj'> {
  /** 图的所有边 */
  edges: () => Iterable<Edge>
  /** adjacency 返回和 v 相邻的所有边 */
  adj: (v: number) => Iterable<Edge>
}

实现：

class Edge implements EdgeBase {
  private _weight: number

  private v: number

  private w: number

  weight() {
    return this._weight
  }

  either() {
    return this.v
  }

  other(vertex: number) {
    if (vertex === this.v) {
      return this.w
    }
    if (vertex === this.w) {
      return this.v
    }
    throw Error()
  }

  constructor(v: number, w: number, weight: number) {
    this.v = v
    this.w = w
    this._weight = weight
  }

  compareTo(that: Edge) {
    if (this.weight() < that.weight()) {
      return -1
    }
    if (this.weight() > that.weight()) {
      return 1
    }
    return 0
  }
}

class EdgeWeightedGraph implements EdgeWeightedGraphBase {
  private v: number

  private e: number

  private adjList: Array<LinkedList<Edge>>

  constructor(v: number) {
    this.v = v
    this.e = 0
    this.adjList = new Array(v)

    for (let i = 0; i < v; i++) {
      this.adjList[i] = new LinkedList<Edge>()
    }
  }

  V() {
    return this.v
  }

  E() {
    return this.e
  }

  addEdge(e: Edge) {
    const v = e.either()
    const w = e.other(v)
    this.adjList[v].push(e)
    this.adjList[w].push(e)
    this.e++
  }

  adj(v: number) {
    return this.adjList[v]
  }

  edges() {
    const edges = new LinkedList<Edge>()
    for (let v = 0; v < this.V(); v++) {
      for (const e of this.adjList[v]) {
        if (e.other(v) > v) {
          edges.push(e)
        }
      }
    }
    return edges
  }
}

最小生成树的表示

一幅加权图的最小生成树是他的子图，也同时是一颗树。

几种表示方式：

一组边的列表
一幅加权无向图
一个以顶点为索引且含有父结点链接的数组

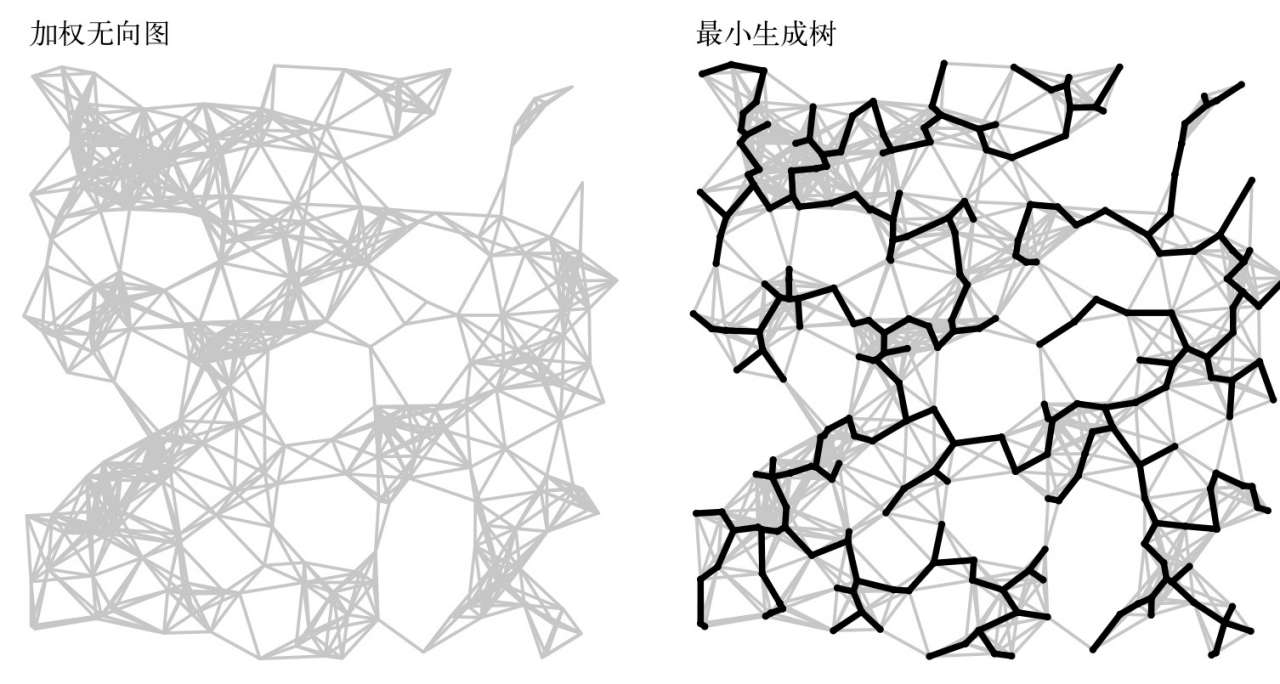
举例：下图是一幅含有250个顶点的无向加权欧几里得图（共含有1273条边）和它的最小生成树

API 表示

interface MST {
  /** 最小生成树的所有边 */
  edges: () => Iterable<Edge>
  /** 最小生成树的权重 */
  weight: () => number
}

Prim 算法

Prim算法它的每一步都会为一棵生长中的树添加一条边。一开始这棵树只有一个顶点，然后会向它添加V-1条边，每次总是将下一条连接树中的顶点与不在树中的顶点且权重最小的边。

Prim算法能够得到任意加权连通图的最小生成树。

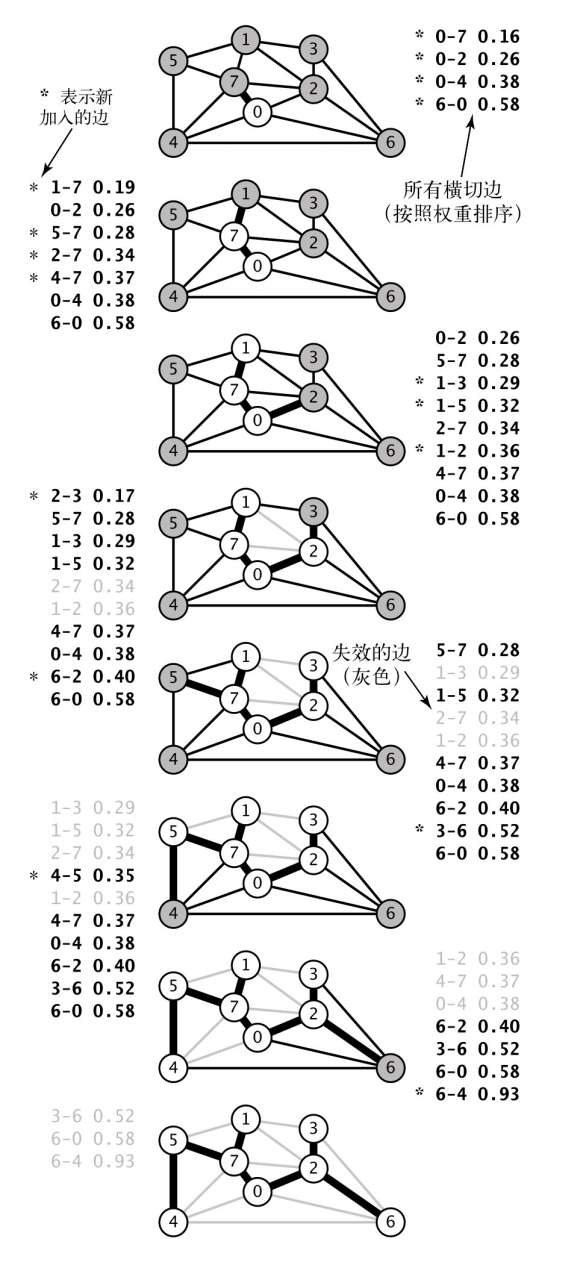
prim 算法过程：

从顶点 0 开始，将顶点 0 添加到 MST，将 0 的邻接表中的边按优先级队列排列（0-7 是最小的）
将顶点 7 和边 0-7 添加到 MST，将 7 的邻接表中的边添加到优先级队列（1-7 是最小的）
将顶点 1 和边 1-7 添加到 MST，将 1 的邻接表中的边添加到优先级队列（0-2 是最小的）
将顶点 2 和边 0-2 添加到 MST，将 2 的邻接表中的边添加到优先级队列（将 2-7、1-2 置为失效，因为顶点 1 和 7 已经在 MST 中了。2-3 是最小的）
。。。
直到结束

prim 算法的延时实现运行时间：所需空间与 E (边的数量）成正比，所需时间与ElogE 成正比。

注：这里还可以做优化，我们不需要在优先级队列中保存所有的边，两个顶点已经失效的边如上的 2-7、1-2 已经没用了。

注：未优化前叫延时实现，优化后叫即时实现，区别在于上述的失效的边会被删除掉。不是很理解他说的延时、即时的说法，无非优化后的占用空间小点，时间快点。

Prim算法的即时实现计算一幅含有V个顶点和E条边的连通加权无向图的最小生成树所需的空间和V成正比，所需的时间和ElogV成正比（最坏情况）。

具体实现如下：

public class PrimMST
{
    private Edge[] edgeTo;           // 距离树最近的边
    private double[] distTo;         // distTo[w]=edgeTo[w].weight()
    private boolean[] marked;        // 如果v在树中则为true
    private IndexMinPQ＜Double＞ pq;  // 有效的横切边
    public PrimMST(EdgeWeightedGraph G)
    {
      edgeTo = new Edge[G.V()];
      distTo = new double[G.V()];
      marked = new boolean[G.V()];
      for (int v = 0; v ＜ G.V(); v++)
          distTo[v] = Double.POSITIVE_INFINITY;
      pq = new IndexMinPQ＜Double＞(G.V());
      distTo[0] = 0.0;
      pq.insert(0, 0.0);                // 用顶点0和权重0初始化pq
      while (! pq.isEmpty())
          visit(G, pq.delMin());        // 将最近的顶点添加到树中
    }
    private void visit(EdgeWeightedGraph G, int v)
    {  // 将顶点v添加到树中，更新数据
      marked[v] = true;
      for (Edge e : G.adj(v))
      {
          int w = e.other(v);
          if (marked[w]) continue;      // v-w失效
          if (e.weight() ＜ distTo[w])
          {  // 连接w和树的最佳边Edge变为e
            edgeTo[w] = e;
            distTo[w] = e.weight();
            if (pq.contains(w)) pq.change(w, distTo[w]);
            else                  pq.insert(w, distTo[w]);
          }
      }
    }
    public Iterable＜Edge＞ edges()
    public double weight()
}

Kruskal算法

主要思想是按照边的权重顺序（从小到大）处理它们，将边加入最小生成树中（图中的黑色边），加入的边不会与已经加入的边构成环，直到树中含有V-1条边为止。

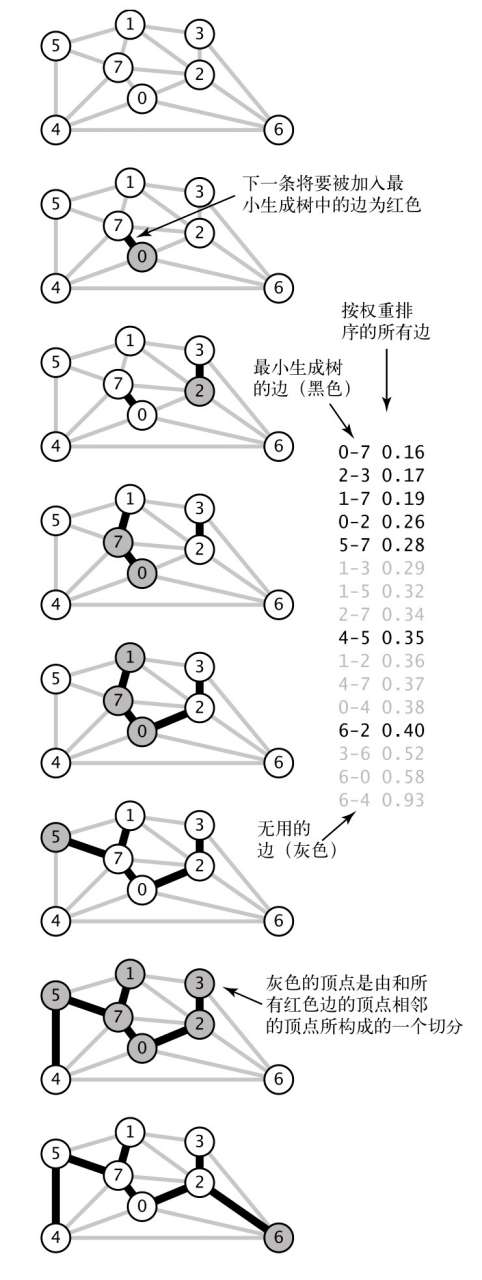
public class KruskalMST
{
    private Queue＜Edge＞ mst;
    public KruskalMST(EdgeWeighMSTtedGraph G)
    {
      mst = new Queue＜Edge＞();
      MinPQ＜Edge＞ pq = new MinPQ＜Edge＞();
      for(Edge e:G.edges())pq.insert(e);
      UF uf = new UF(G.V());
      while (! pq.isEmpty() && mst.size() ＜ G.V()-1)
      {
      MST Edge e = pq.delMin();              // 从pq得到权重最小的边和它的顶点
          int v = e.either(), w = e.other(v);
          if (uf.connected(v, w)) continue;   // 忽略失效的边
          uf.union(v, w);                       // 合并分量
          mst.enqueue(e);                       // 将边添加到最小生成树中
      }
    }
    public Iterable＜Edge＞ edges()
    {  return mst;  }
    public double weight() 
}

加权图（最小生成树）

加权图的表示​

最小生成树的表示​

Prim 算法​

Kruskal算法​

加权图的表示

最小生成树的表示

Prim 算法

Kruskal算法