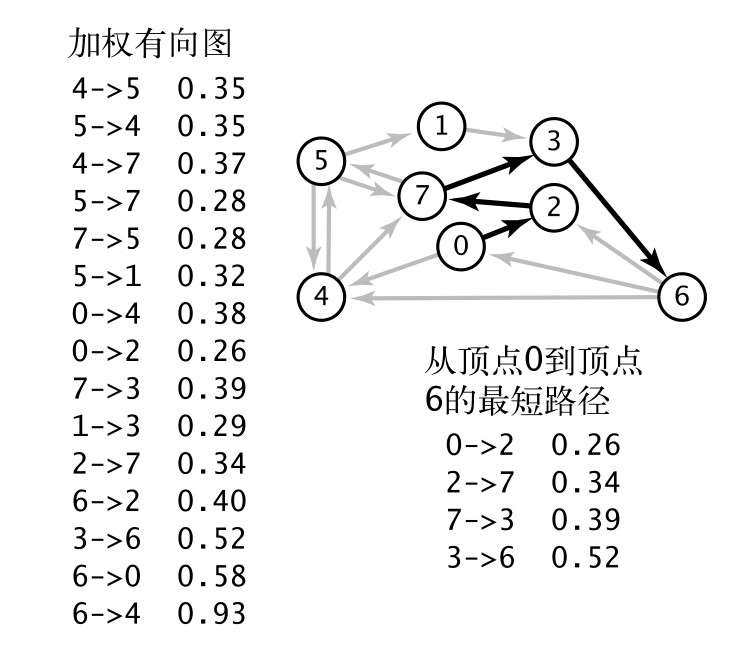
加权有向图（最短路径）

加权有向图最直观的处理问题就是地点A 到地点B 的路径，在这个模型中，问题被归纳为：找到从一个顶点到达另一个顶点的成本最小的路径。

应用：

最短路径

最短路径：在一幅加权有向图中，从顶点s到顶点t的最短路径是所有从s到t的路径中的权重最小者。

性质：

• 路径是有向的
• 权重不一定指距离
• 并得所有顶点可达
• 负权重会带来更复杂的问题（我们只讨论正的或零）
• 最短路径一般都是简单的（我们的算法忽略环）
• 最短路径不是唯一的（我们只要找到一条即可）
• 可能存在平行边或自环（我们的讨论假设不存在平行边，也会忽略自环）

最短路径树：给定一幅加权有向图和一个顶点s，以s为起点的一棵最短路径树是图的一幅子图，它包含s和从s可达的所有顶点。这棵有向树的根结点为s，树的每条路径都是有向图中的一条最短路径。

加权有向图的数据结构

定义

// 加权有向边
interface DirectedEdge {
  /** 边的权重 */
  weight: () => number
  /** 起时顶点 */
  from: () => number
  /** 目标顶点 */
  to: (v: number) => number
}

// 加权有向图
interface EdgeWeightedDigraph {
  /** vertex 顶点数 */
  V: () => number
  /** edge 边数 */
  E: () => number
  /** 图的所有边 */
  edges: () => Iterable<DirectedEdge>
  /** adjacency 返回和 v 相邻的所有边 */
  addEdge: (e: DirectedEdge) => void
  /** adjacency 返回和 v 相邻的所有边 */
  adj: (v: number) => Iterable<DirectedEdge>
}

实现

class DirectedEdge implements DirectedEdgeBase {
  private _weight: number

  private v: number

  private w: number

  from() {
    return this.v
  }

  to() {
    return this.w
  }

  weight() {
    return this._weight
  }

  constructor(v: number, w: number, weight: number) {
    this.v = v
    this.w = w
    this._weight = weight
  }
}

class EdgeWeightedDigraph implements EdgeWeightedDigraphBase {
  private v: number

  private e: number

  private adjList: Array<LinkedList<DirectedEdge>>

  constructor(v: number) {
    this.v = v
    this.e = 0
    this.adjList = new Array(v)

    for (let i = 0; i < v; i++) {
      this.adjList[i] = new LinkedList<DirectedEdge>()
    }
  }

  V() {
    return this.v
  }

  E() {
    return this.e
  }

  addEdge(e: DirectedEdge) {
    this.adjList[e.from()].push(e)
    this.e++
  }

  adj(v: number) {
    return this.adjList[v]
  }

  edges() {
    const edges = new LinkedList<DirectedEdge>()
    for (let v = 0; v < this.V(); v++) {
      for (const e of this.adjList[v]) {
        edges.push(e)
      }
    }
    return edges
  }
}

最短路径

对于术语松弛的理解：原本橡皮筋连接在 p-v 上，通过将橡皮筋转移到另一条更短的路径上 w-v 来缓解橡皮筋的压力。

边的松弛

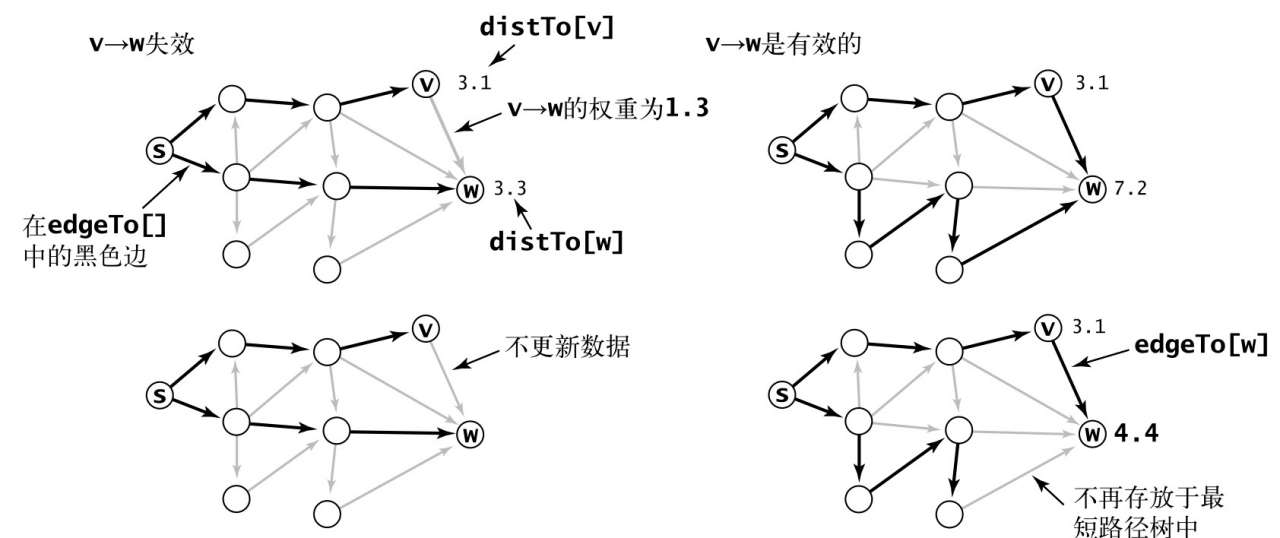
private edgeRelax(e: DirectedEdge) {
  const v = e.from()
  const w = e.to()
  if (this._distTo[w] > this._distTo[v] + e.weight()) {
    this._distTo[w] = this._distTo[v] + e.weight()
    this._edgeTo[w] = e
  }
}

顶点的松弛

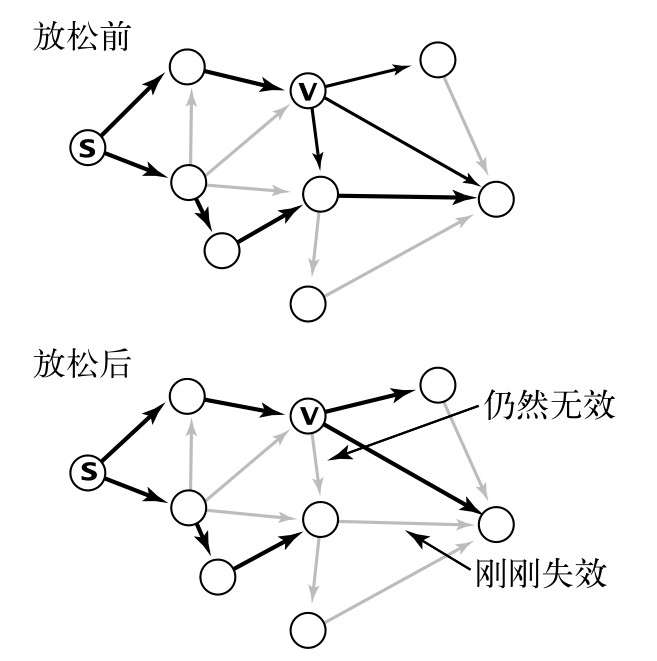
private vertexRelax(G: EdgeWeightedDigraph, v: number) {
  for (const e of G.adj(v)) {
    const w = e.to()

    if (this._distTo[w] > this._distTo[v] + e.weight()) {
      this._distTo[w] = this._distTo[v] + e.weight()
      this._edgeTo[w] = e
    }
  }
}

查询API

/** 从顶点 S 到顶点 V 的距离，如果不存在则无限大 */
distTo(v: number) {
  return this._distTo[v]
}

/** 是否存在从顶点 S 到顶点 V 的路径 */
hasPathTo(v: number) {
  return this._distTo[v] < Number.POSITIVE_INFINITY
}

/** 从顶点 S 到顶点 V 的路径 */
pathTo(v: number) {
  if (!this.hasPathTo(v)) {
    return null
  }
  const path = new Stack<DirectedEdge>()

  for (let e = this._edgeTo[v]; e != null; e = this._edgeTo[e.from()]) {
    path.push(e)
  }
  return path
}

通用的最短路径算法：

将distTo[s]初始化为0，其他distTo[]元素初始化为无穷大，继续如下操作：放松G中的任意边，直到不存在有效边为止。对于任意从s可达的顶点w，在进行这些操作之后，distTo[w]的值即为从s到w的最短路径的长度（且edgeTo[w]的值即为该路径上的最后一条边）。

最短路径的Dijkstra算法

public class DijkstraS {
  private DirectedEdge[] edgeTo;
  private double[] distTo;
  private IndexMinPQ＜Double＞ pq;
  public DijkstraSP(EdgeWeightedDigraphG, int s) {
    edgeTo = new DirectedEdge[G.V()];
    distTo = new double[G.V()];
    pq = new IndexMinPQ＜Double＞(G.V());
    for (int v = 0; v ＜ G.V(); v++)
      distTo[v] = Double.POSITIVE_INFINITY;
    distTo[s] = 0.0;
    pq.insert(s, 0.0);
    while (!pq.isEmpty())
      relax(G, pq.delMin())
  }
  private void relax(EdgeWeightedDigraph G, int v) {
    for(DirectedEdge e : G.adj(v))
    {
      int w = e.to();
      if (distTo[w] ＞ distTo[v] + e.weight())
      {
        distTo[w] = distTo[v] + e.weight();
        edgeTo[w] = e;
        if (pq.contains(w)) pq.change(w, distTo[w]);
        else pq.insert(w, distTo[w]);
      }
    }
  }

  // 见上方 TS 实现的 API 查询
  public double distTo(int v) 
  public boolean hasPathTo(int v) 
  public Iterable＜DirectedEdge＞ pathTo(int v)
}

无环加权有向图中的最短路径算法

许多应用中的加权有向图都是不含有有向环的，学习一种比Dijkstra算法更快、更简单的在无环加权有向图中找出最短路径的算法。

• 能够在线性时间内解决单点最短路径问题
• 能够处理负权重的边
• 能够解决相关的问题，例如找出最长的路径

按照拓扑顺序放松顶点，就能在和 E + V 成正比的时间内解决无环加权有向图的单点最短路径问题。

因为它的“无环”能够极大地简化问题的论断。

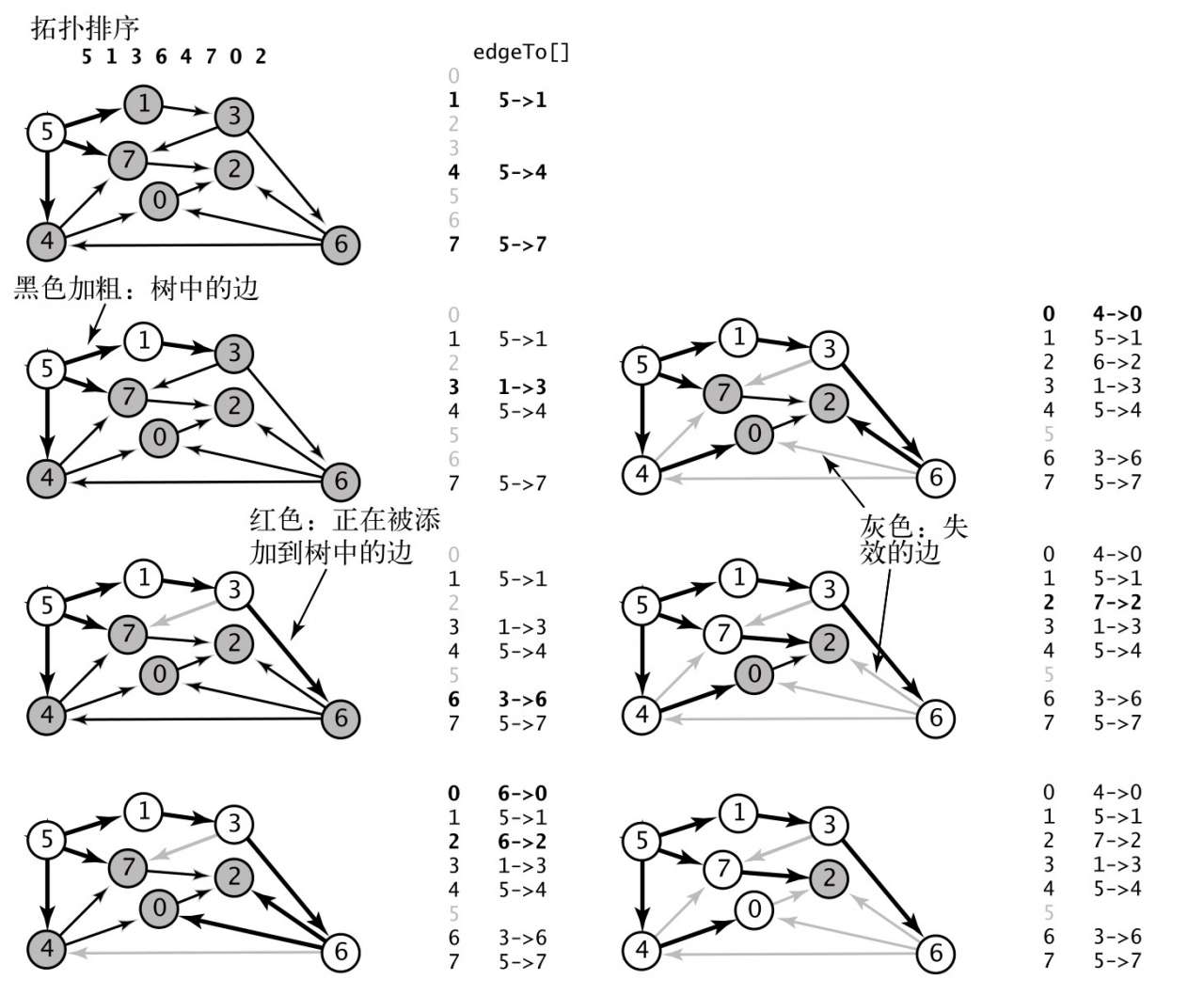
• 用深度优先搜索得到图的顶点的拓扑排序5 1 3 6 4 7 0 2；
• 将顶点5和从它指出的所有边添加到树中；
• 将顶点1和边1→3添加到树中；
• 将顶点3和边3→6添加到树中，边3→7已经失效；
• 将顶点6和边6→2、6→0添加到树中，边6→4已经失效；
• 将顶点4和边4→0添加到树中，边4→7和6→0已经失效；
• 将顶点7和边7→2添加到树中，边6→2已经失效；
• 将顶点0添加到树中，边0→2已经失效；
• 将顶点2添加到树中。

public class AcyclicSP
{
    private DirectedEdge[] edgeTo;
    private double[] distTo;
    public AcyclicSP(EdgeWeightedDigraph G, int s)
    {
      edgeTo = new DirectedEdge[G.V()];
      distTo = new double[G.V()];
      for (int v = 0; v ＜ G.V(); v++)
          distTo[v] = Double.POSITIVE_INFINITY;
      distTo[s] = 0.0;
      Topological top = new Topological(G);
      for (int v : top.order())
          relax(G, v);
  }
  private void relax(EdgeWeightedDigraph G, int v)
  public double distTo(int v) 
  public boolean hasPathTo(int v)
  public Iterable＜DirectedEdge＞ pathTo(int v)
}

最长路径

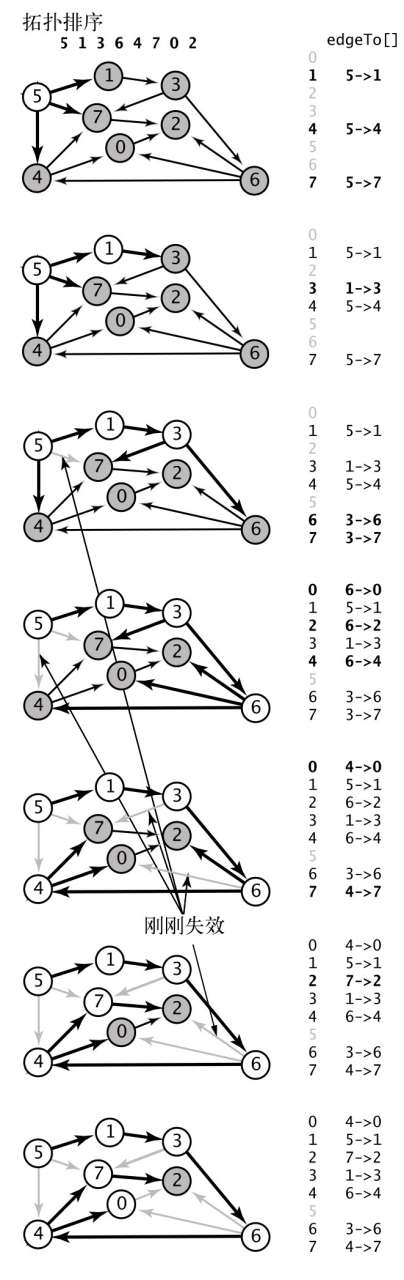
• 用深度优先搜索得到图的顶点的拓扑排序5 1 3 6 4 7 0 2；
• 将顶点5和从它指出的所有边添加到树中；
• 将顶点1和边1→3添加到树中；
• 将顶点3和边3→6、3→7添加到树中，边5→7已经失效；
• 将顶点6和边6→2、6→4和6→0添加到树中，边5→4已经失效；
• 将顶点4和边4→0、4→7添加到树中，边6→0和3→7已经失效；
• 将顶点7和边7→2添加到树中，边6→2已经失效；
• 将顶点0添加到树中，边0→2已经失效；
• 将顶点2添加到树中（未画出）。

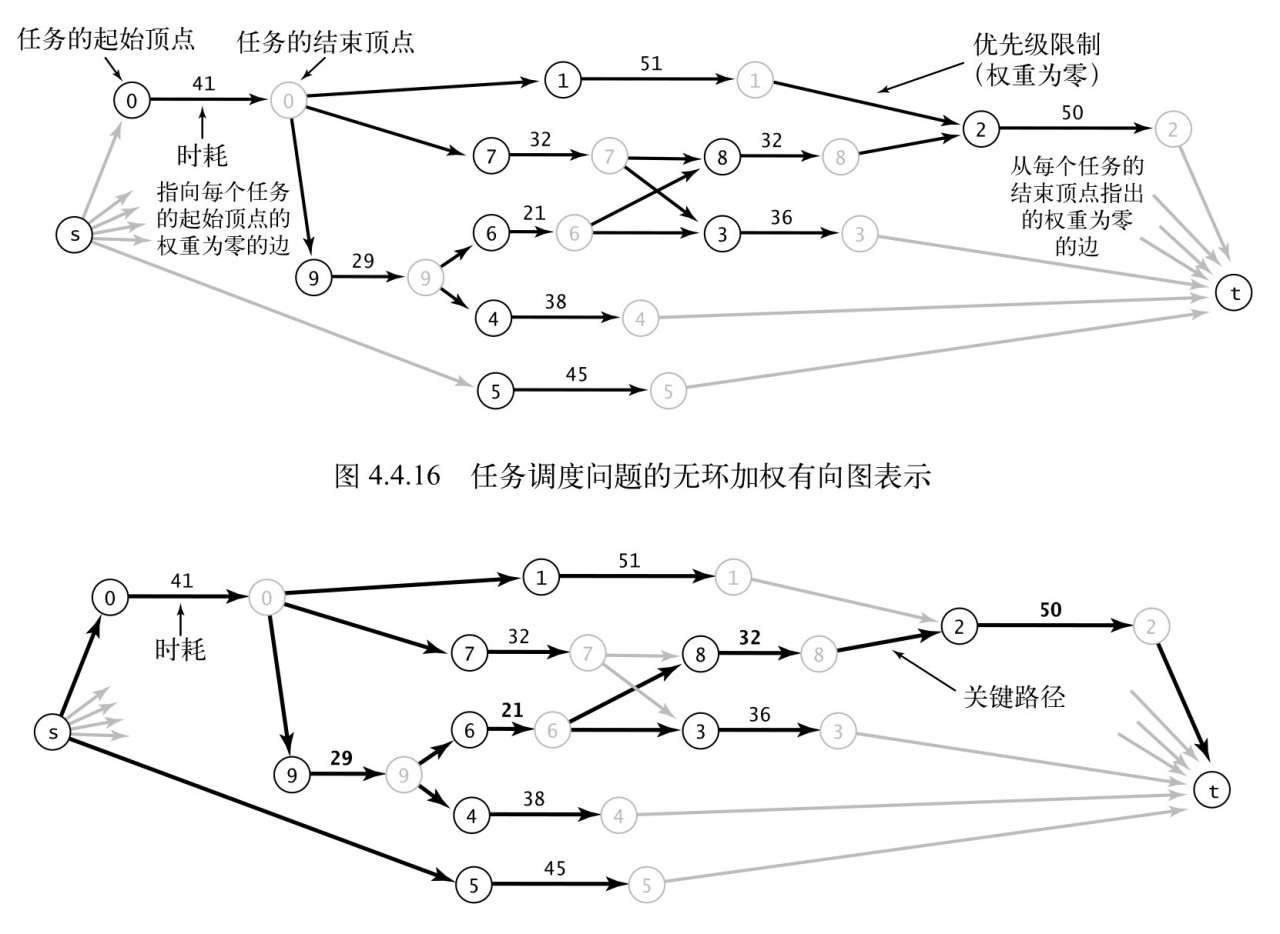
并行任务调度

这里实现的任务调度问题的关键路径方法将问题归约为寻找无环加权有向图的最长路径问题

public class CPM
{
    public static void main(String[] args)
    {
      int N = StdIn.readInt(); StdIn.readLine();
      EdgeWeightedDigraph G;
      G = new EdgeWeightedDigraph(2＊N+2);
      int s = 2＊N, t = 2＊N+1;
      for (int i = 0; i ＜ N; i++)
      {
          String[] a = StdIn.readLine().split("\\s+");
          double duration = Double.parseDouble(a[0]);
          G.addEdge(new DirectedEdge(i, i+N, duration));
          G.addEdge(new DirectedEdge(s, i, 0.0));
          G.addEdge(new DirectedEdge(i+N, t, 0.0));
          for (int j = 1; j ＜ a.length; j++)
          {
            int successor = Integer.parseInt(a[j]);
            G.addEdge(new DirectedEdge(i+N, successor, 0.0));
          }
      }
      AcyclicLP lp = new AcyclicLP(G, s);
      StdOut.println("Start times:");
      for (int i = 0; i ＜ N; i++)
          StdOut.printf("%4d: %5.1f\n", i, lp.distTo(i));
      StdOut.printf("Finish time: %5.1f\n", lp.distTo(t));
  }
}

相对最后期限限制下的并行任务调度

一般加权有向图中的最短路径问题

• 基于队列的Bellman-Ford算法
• 负权重的边
• 负权重环的检测
• 套汇