无向图
定义
定义:
顶点(vertex):图中的一个节点
边(edge):(在无向图中)是两个顶点之间的连接。
图:是由一组顶点和一组(能够将两个顶点相连的)边组成的。
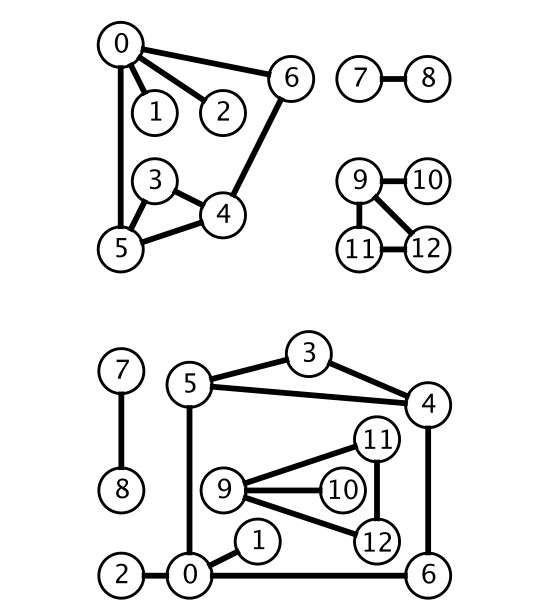
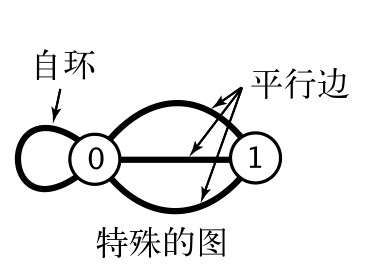
(会有实际应用使用自环和平行边,但不在当前讨论范围内。)
- 含有平行边的图叫做多重图
- 没有平行边或自环的图叫做简单图
定义:
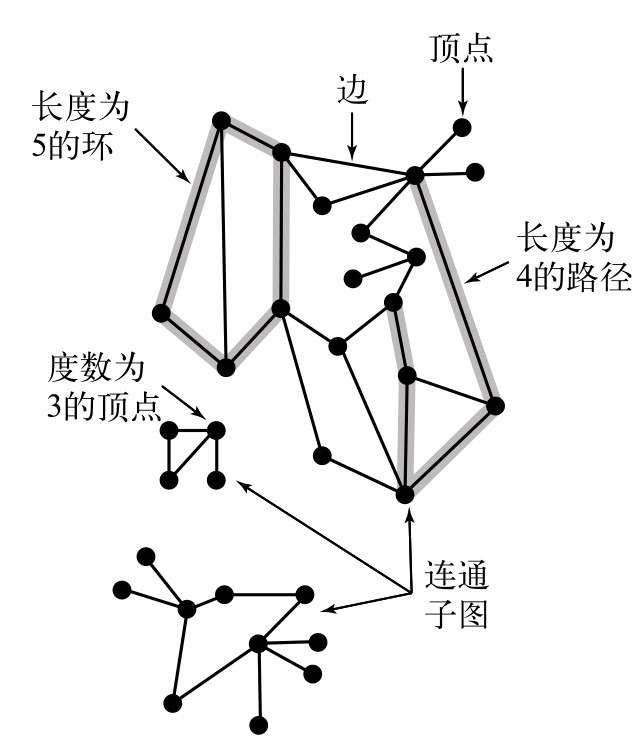
顶点的度数:为依附于它的边的总数。
路径:是由边顺序连接的一系列顶点。
简单路径:是一条没有重复顶点的路径。
环:是一条至少有一条边,且起点终点相同的路径。
简单环:是一条(除了起点终点)不含有重复顶点和边的环。
我们主要研究简单路径、简单环,并省略“简单”二字。
我们用 u-v-w-x 记法表示 u 到 x 的路径
用 u-v-w-x-u 表示 u 到 x 再到 u 的一条环
定义:
连通图:如果从任意一个顶点都存在一条路径到达另一个任意顶点,我们称这幅图是连通图。
一幅非连通的图由若干连通的部分组成,它们都是其极大连通子图。
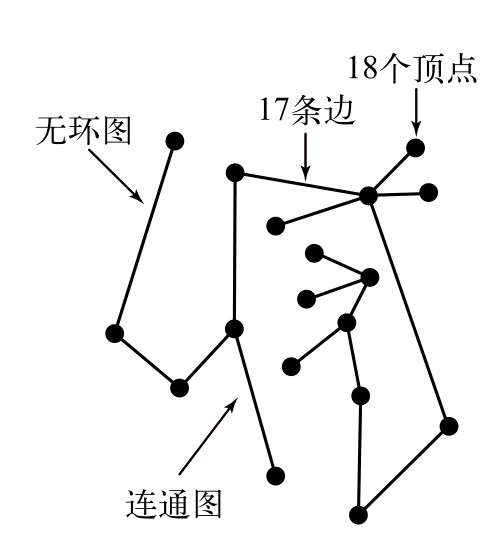
无环图:是一种不包含环的图。
树:是一副无环连通图。
森林:是互不相连的树组合成的集合
【树的定义非常通用,稍做改动就可以变成用来描述程序行为的(函数调用层次)模型和数据结构(二叉查找树、2-3树等)】
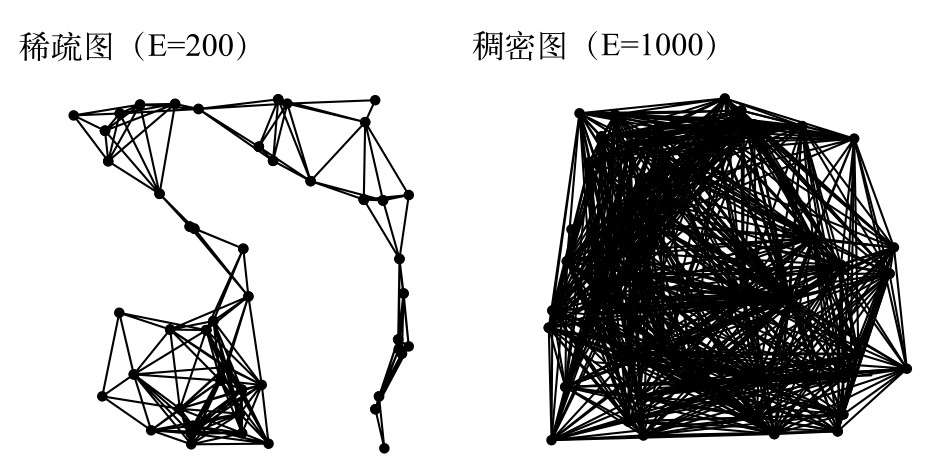
图的密度:是指已经连接的顶点对占所有可能被连接的顶点对的比例。
二分图:是一种能够将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分。
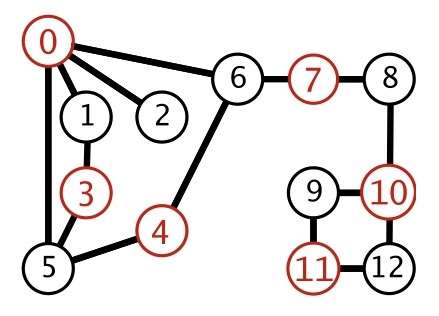
无向图的数据类型表示
API 定义
interface Graph {
/** vertex 顶点数 */
V: () => number
/** edge 边数 */
E: () => number
/** 向图中添加一条 v-w 的边 */
addEdge: (v: number, w: number) => void
/** 返回和 v 相邻的所有顶点 */
adj: (v: number) => Iterable<Number>
/** 对象的字符串表示 */
toSting: () => string
}
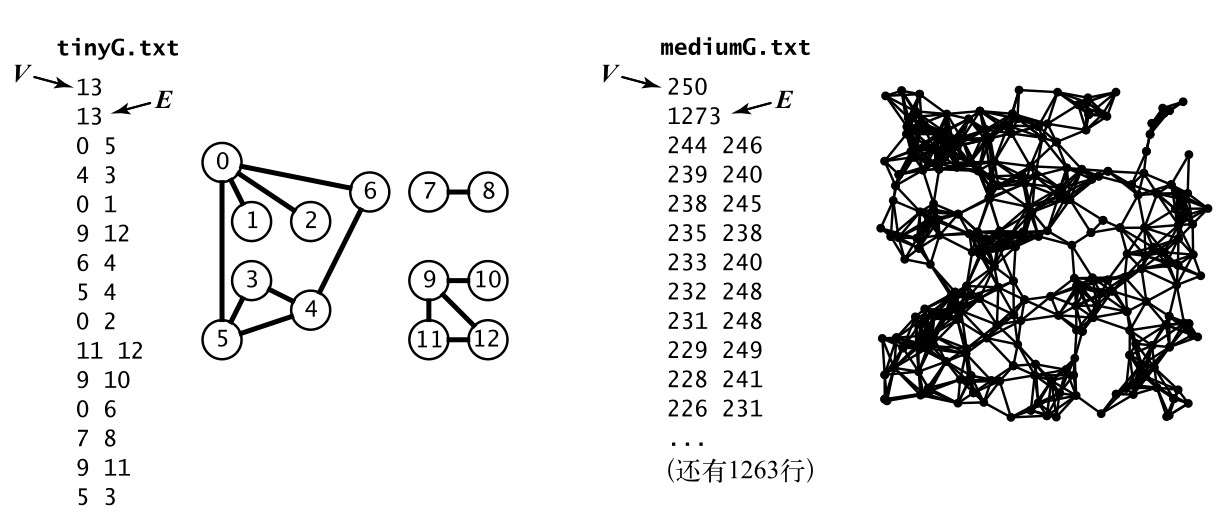
常用的处理代码:
图的表示方式
实现要求:
- 必须为可能在应用中碰到的各种类型的图预留出足够的空间
- Graph 的实例方法的实现一定要快
三种图的表示方法:
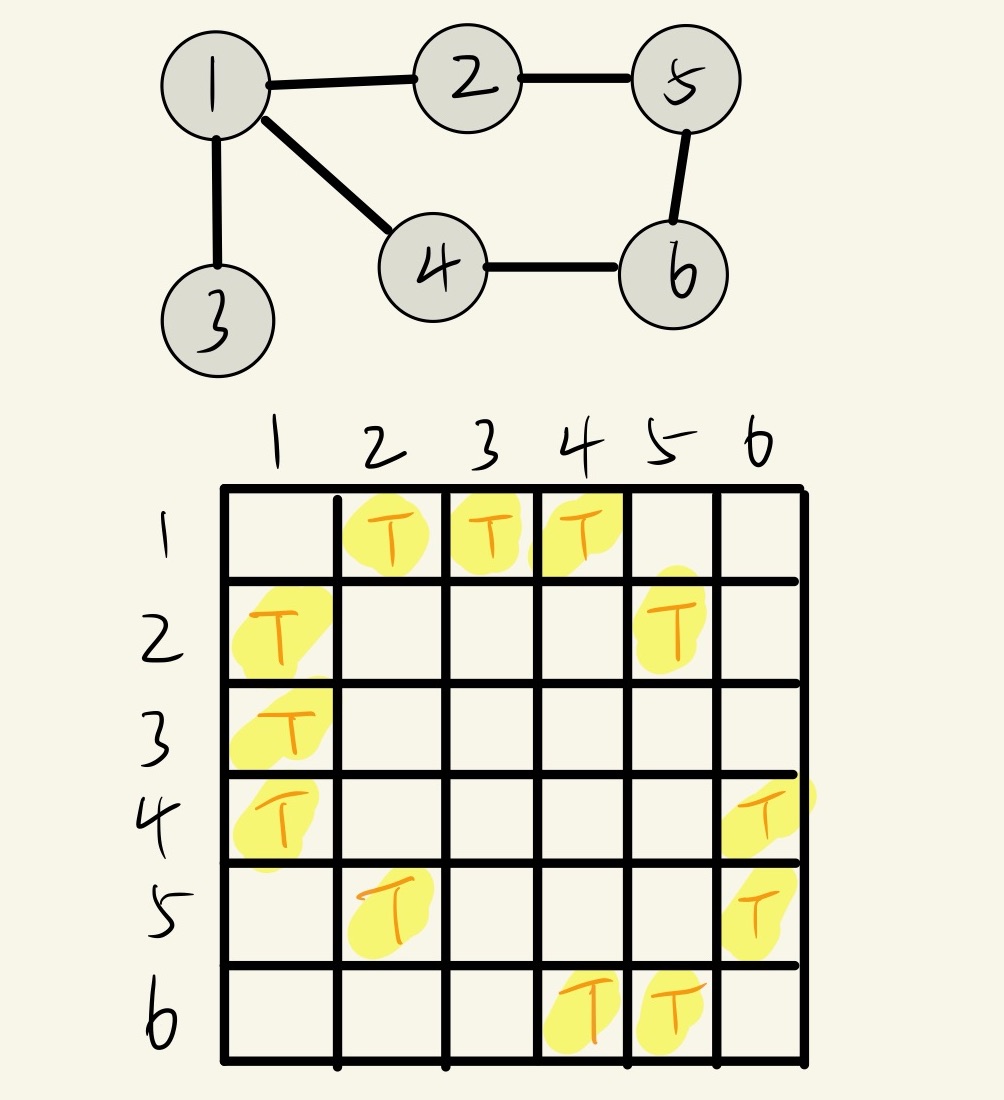
邻接矩阵:可以使用一个 V * V 的布尔矩阵,当顶点 v 和顶点 w 之间有相连接的边时,定义 v 行 w 列的元素值为 true,否则为 false。
如果图是稠密(dense)的,邻接矩阵是合适的表示方式(但大部分应用并非如此)【数据结构与算法分析】
缺点:
不符合第一个要求,含有上百万个顶点的图很常见,v的2次方个布尔值占用空间太大
无法表达平行边
边的数组:定义一个包含两个数值(顶点)的 Edge 类,生成
Array<Edge>。- 表示方式简洁
- 缺点:
- 不能满足第二个条件,比如实现
adj()方法会很麻烦
- 不能满足第二个条件,比如实现
邻接表(adjacency list)(数组):使用一个以顶点为索引的数组,其中的每个元素都是和该顶点相邻的顶点集合,这里的集合指的是无序集。(《算法 第4版》里叫做列表,并使用了
Bag抽象数据类型,wiki 中叫集合,感觉集合更通用点)一般这个集合我们用链表实现(后续例子都会按链表实现),也可以使用数组,为了提高查找效率甚至可以使用平衡二叉叉招数、红黑树等方式实现。(个人理解)
- 使用的空间和 V + E 成正比
- 添加一条边的时间为常数(有待探讨,原文中,Bag 的新增一条数据时间复杂度是常数的,而链表的新增是 O(n) )
- 遍历顶点 v 的所有相临顶点所需的时间和 v 的度数成正比(处理每个相邻顶点所需的时间为常数)
- 缺点
- 无法快速判断 v 和 w 是否相邻,而邻接矩阵可以直接
matrix[v][w]
- 无法快速判断 v 和 w 是否相邻,而邻接矩阵可以直接
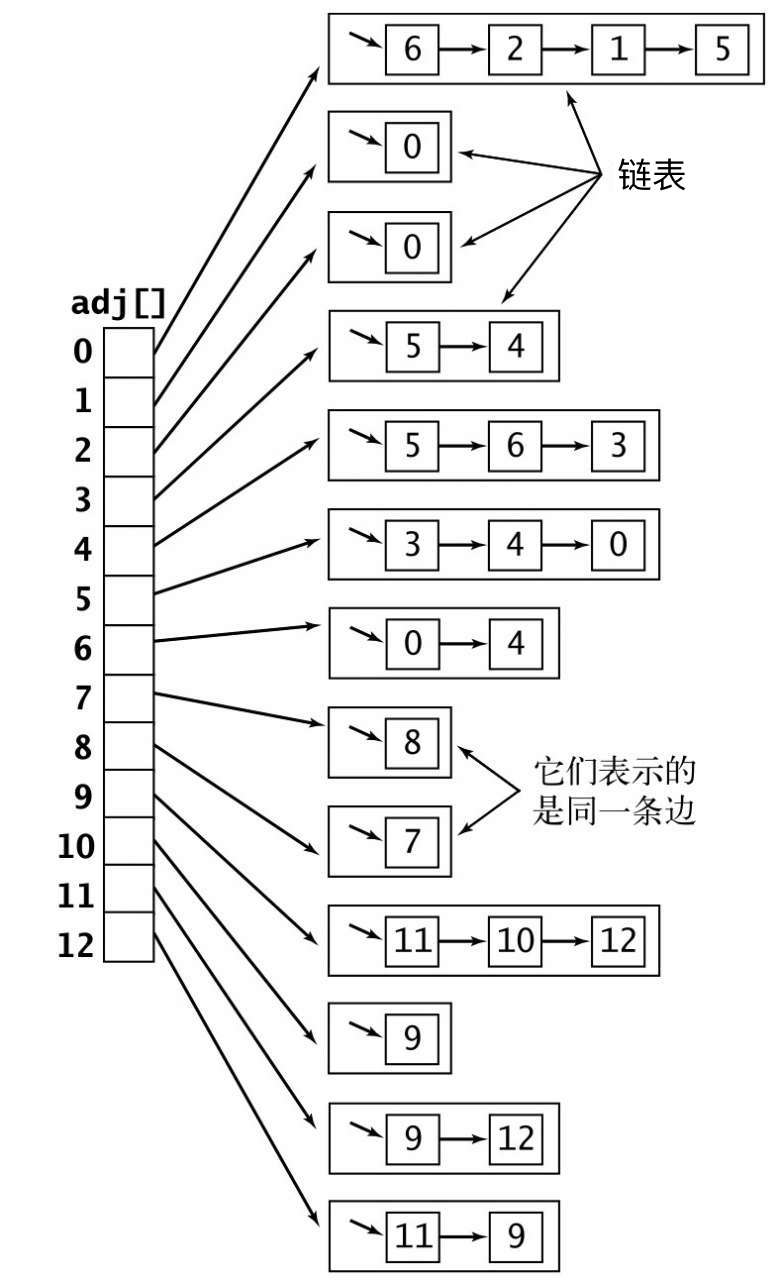
- 邻接集:将上述的集合改用
Set来实现邻接表,称为邻接集。(将会不允许存在平行边)
不同数据结构实现的复杂度:
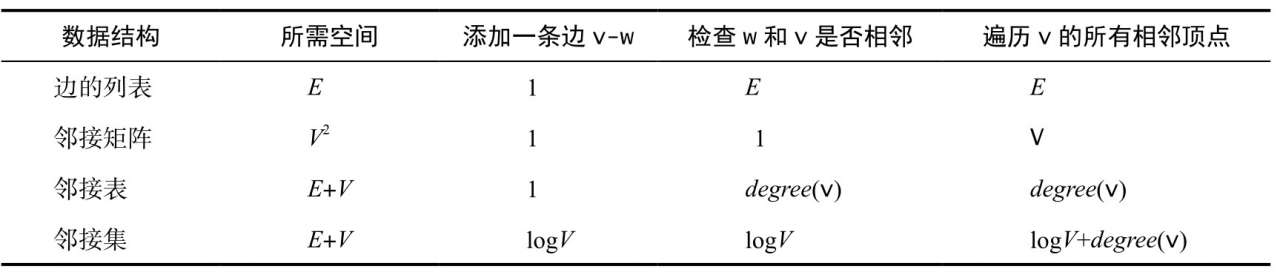
使用邻接表结构的无向图表示
class Graph implements GraphBase {
private v: number
private e: number
private adjList: Array<LinkedList<number>>
constructor(v: number) {
this.v = v
this.e = 0
this.adjList = new Array(v)
for (let i = 0; i < v; i++) {
this.adjList[i] = new LinkedList<number>()
}
}
V() {
return this.v
}
E() {
return this.e
}
addEdge(v: number, w: number) {
this.adj[v].push(w)
this.adj[w].push(v)
this.e++
}
adj(v: number) {
return this.adjList[v]
}
}
应用与算法实现
因为我们会讨论大量关于图处理的算法,所以设计的首要目标是将图的表示和实现分离开来
深度优先搜索(Depth First Search,dfs)
在图中以 start 为起点搜索
class DepthFirstSearch {
private marked: Array<boolean>
constructor(graph: Graph, start: number) {
this.marked = new Array<boolean>(graph.V())
this.dfs(graph, start)
}
private dfs(g: Graph, v: number) {
this.marked[v] = true
for (const w of g.adj(v)) {
if (!this.marked[w]) {
this.dfs(g, w)
}
}
}
}
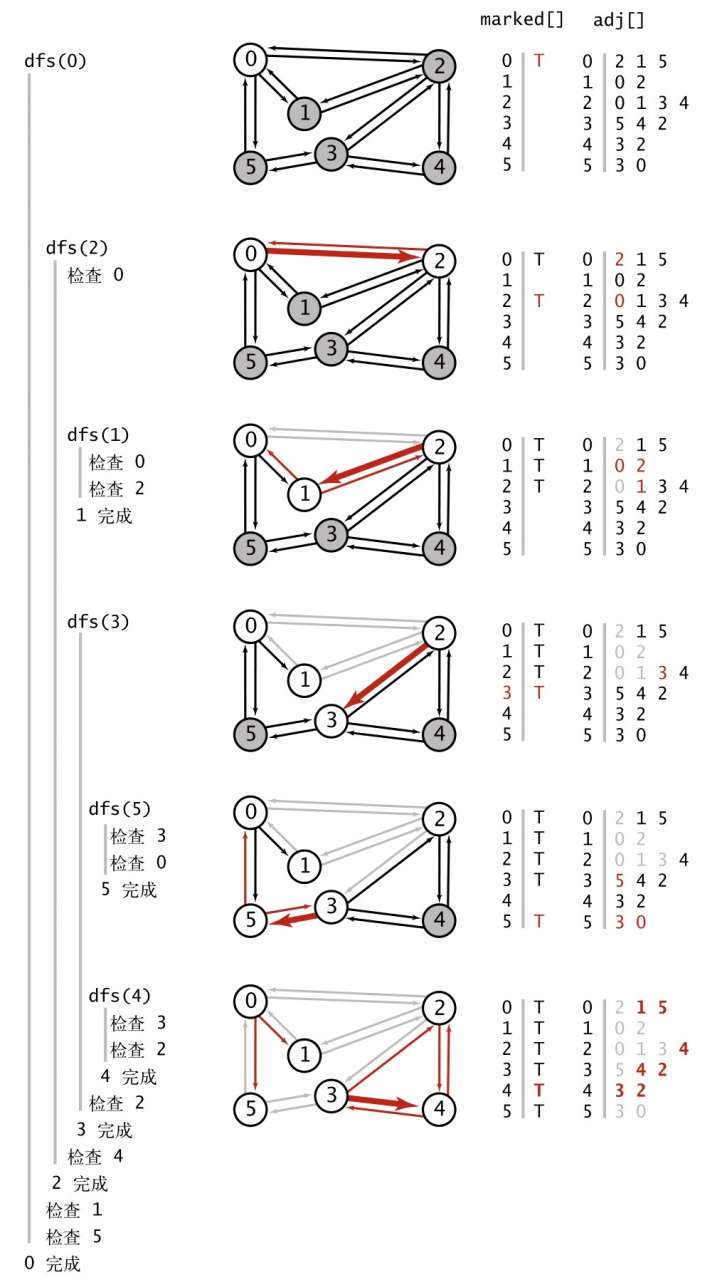
寻找路径(dfs 实现)
在图中找出所有以 start 为起点的路径
class DepthFirstPaths {
private marked: Array<boolean>
// 从起点到一个顶点的已知路径上的最后一个顶点
// edgeTo[w] = v 表示 v-w 是第一次访问 w 时经过的边
private edgeTo: Array<number>
private start: number
constructor(graph: Graph, start: number) {
this.marked = new Array<boolean>(graph.V())
this.edgeTo = new Array<number>(graph.V())
this.start = start
this.dfs(graph, start)
}
private dfs(g: Graph, v: number) {
this.marked[v] = true
for (const w of g.adj(v)) {
if (!this.marked[w]) {
this.edgeTo[w] = v
this.dfs(g, w)
}
}
}
public hasPathTo(v: number) {
return this.marked[v]
}
public pathTo(v: number) {
if (!this.hasPathTo(v)) {
return null
}
const path = []
for (let i = v; i !== this.start; i = this.edgeTo[i]) {
path.unshift(i)
}
path.unshift(this.start)
return path
}
}
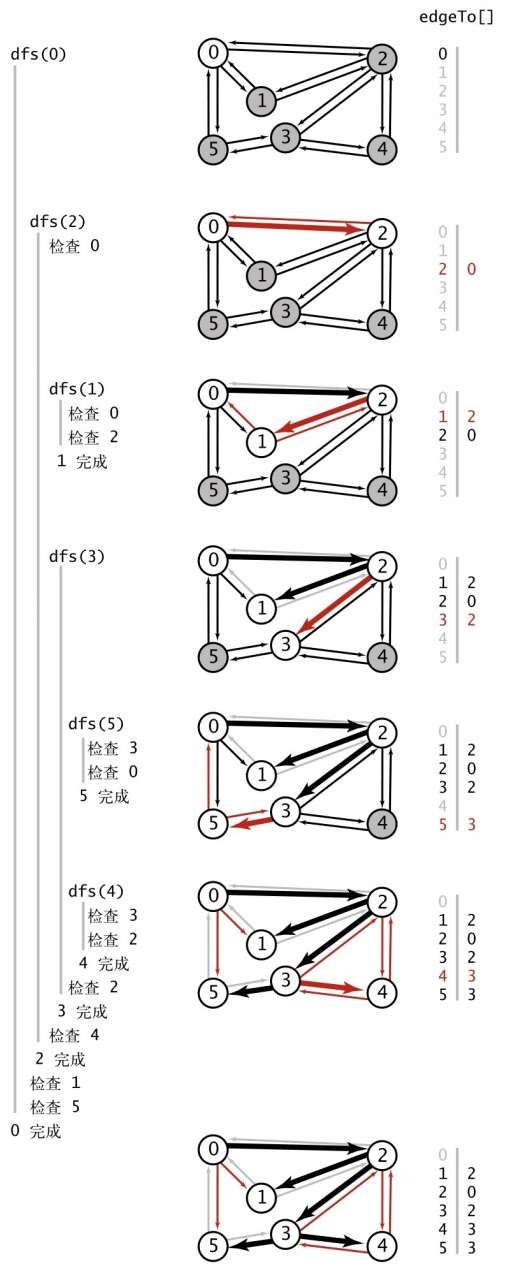
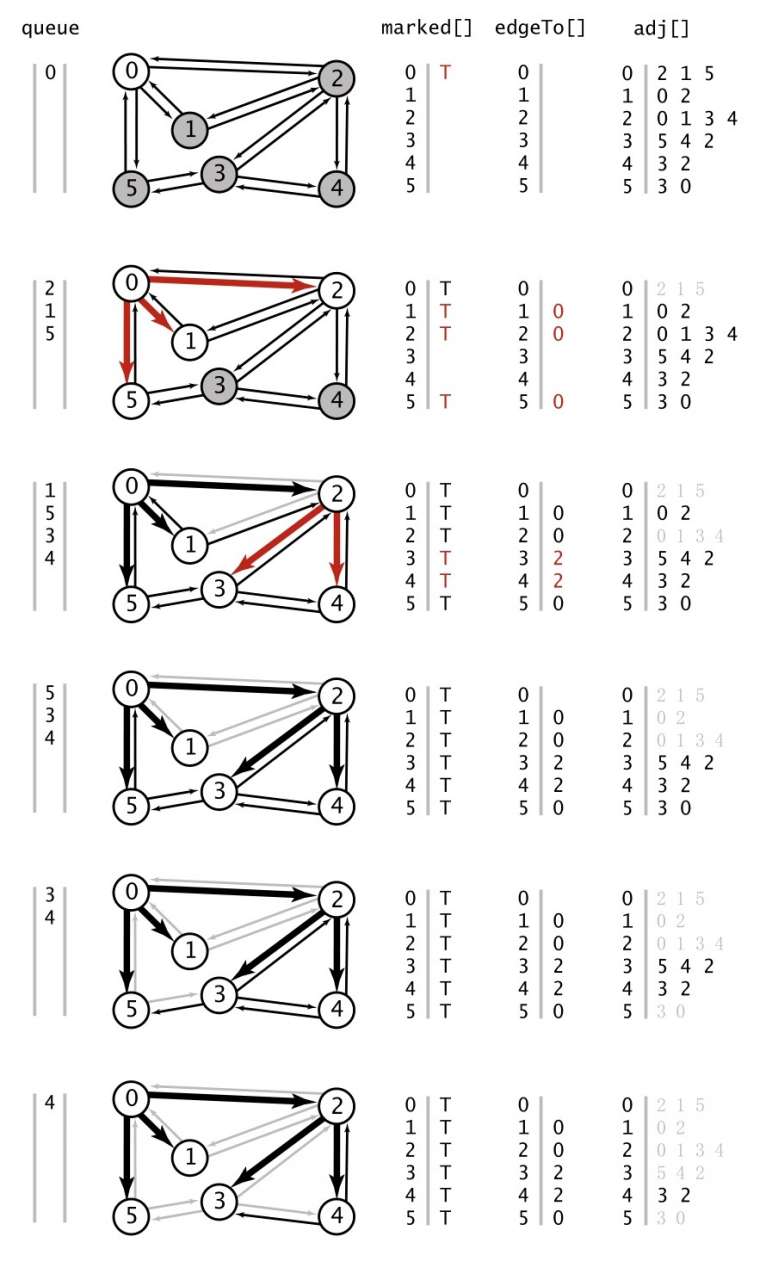
广度优先搜索(Breadth First Search ,bfs),寻找最短路径
探讨的问题:在图中,从起点 s 到目的顶点 v ,是否存在一条路径?如果有,最短路径是多少?
解决这个问题的方式叫做广度优先搜索(bfs)。
dfs 在这个问题上没有作为,遍历整个图的顺序和找出最短路径的目标没有任何关系。(dfs 的 edgeTo 在第一次到达的时候,不一定是最短路径,但后续不会再被改写,bfs 的 edgeTo 在第一次到达的时候,就确定是最短的,后续的也不会被改写)
class BreadthFirstPath {
private marked: Array<boolean>
// 从起点到一个顶点的已知路径上的最后一个顶点
// edgeTo[w] = v 表示 v-w 是第一次访问 w 时经过的边
private edgeTo: Array<number>
private start: number
constructor(graph: Graph, start: number) {
this.marked = new Array<boolean>(graph.V())
this.edgeTo = new Array<number>(graph.V())
this.start = start
this.bfs(graph, start)
}
private bfs(g: Graph, v: number) {
const queue = []
this.marked[v] = true
queue.push(v)
while (queue.length > 0) {
const curV = queue.shift()
for (const w of g.adj(curV)) {
if (!this.marked[w]) {
this.edgeTo[w] = curV
this.marked[w] = true
queue.push(w)
}
}
}
}
// hasPathTo
// pathTo 同 DepthFirstPaths
}
连通分量(Connected Component)(dfs)
深度优先搜索的应用
连通分量:一个图中,连通子图的个数(个人理解)
实现过程其实很简单:
1、遍历数组,marked 标记未标记则 count + 1,开始进入 dfs(dfs 完后,下一次未被标记的就是另一个子图)
2、dfs,dfs 会把当前进入的子图遍历完并 marked,直到退出 dfs 返回步骤1
interface CC {
/** v 和 w 连通吗 */
connected: (v: number, w: number) => boolean
/** 连通分量数 */
count: () => number
/** v 所在的所有连通分量标识符 (0 ~ count-1)*/
id: (v: number) => number
}

(该图的最后一行 id 的表示有点问题,往前挪了一位)
检测环与双色问题(dfs)

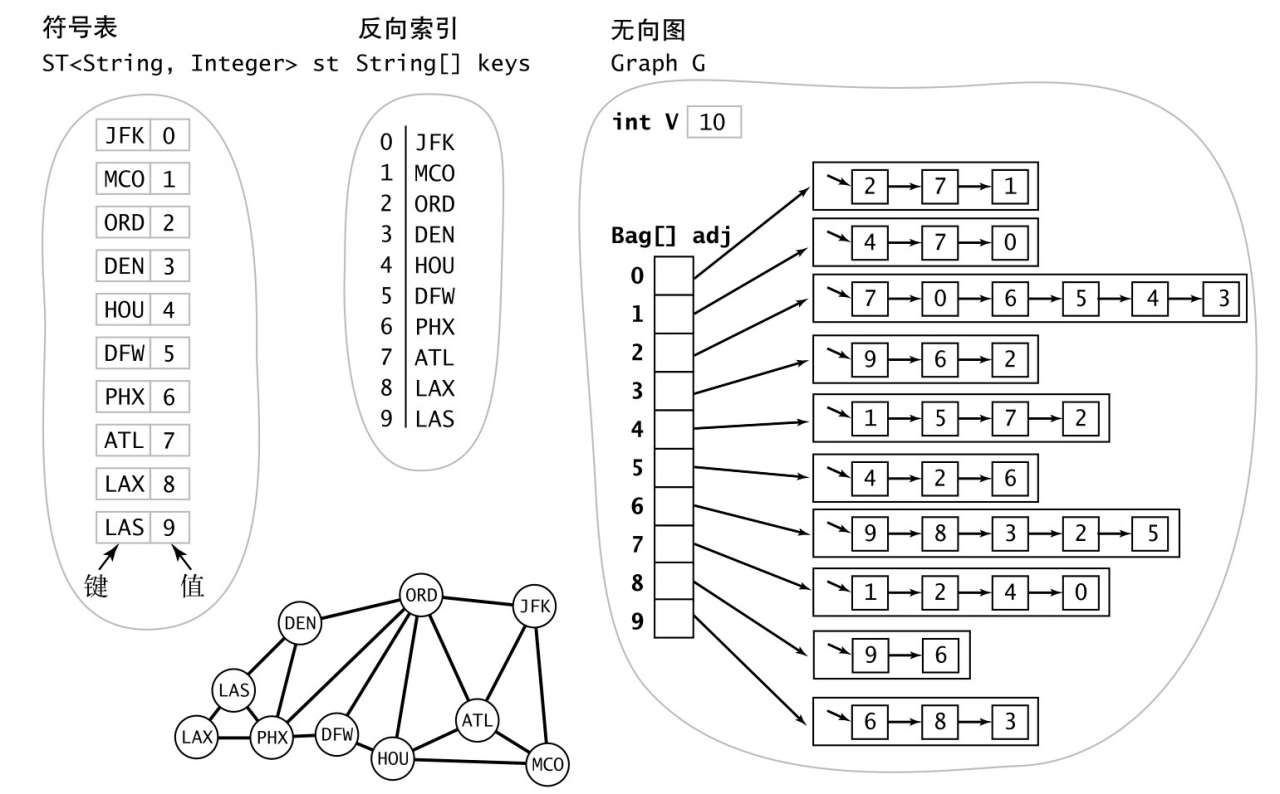
符号图
在实际的应用中,图的顶点可能使用字符串来表示
建立一个 st 符号表,和与之对应的反向索引 keys,之后就都一样了。
间隔的度数
图处理的一个经典问题就是,找到一个社交网络之中两个人间隔的度数。
BFS -> 最短路径