有向图

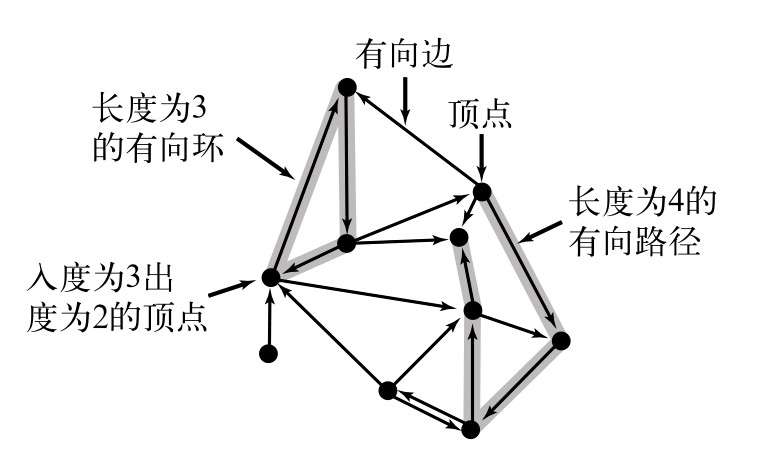
在有向图（directed grapha, digraph）中，边是单向的，每条边所连接的两个顶点都是一个有序对，它们的邻接性是单向的。

有向图的应用：

定义

定义：

有向图：是由一组顶点和一组有方向的边组成的，每条有方向的边都连接着有序的一对顶点。

有向路径：由一系列顶点组成，对于其中的每个顶点都存在一条有向边从它指向序列中的下一个顶点。

有向环：为一条至少含有一条边且起点和终点相同的有向路径。（简单有向环是处理起点终点外，顶点和边都不重复的）

有向图的数据类型

接口定义

interface Digraph extends Graph {
  /** 返回该图的反向图 */
  reverse: () => Digraph
}

在无向图 Graph 的基础上增加了 reverse 方法，在处理有向图时非常有用。

实现细节

// addEdge
addEdge(v: number, w: number) {
  this.adj[v].push(w)
  this.e++
}

// reverse
reverse() {
  const reversedGraph = new Digraph(this.v)

  for (let v = 0; v < this.v; v++) {
    for (const w of this.adj(v)) {
      reversedGraph.addEdge(w, v)
    }
  }
  return reversedGraph
}

应用与算法实现

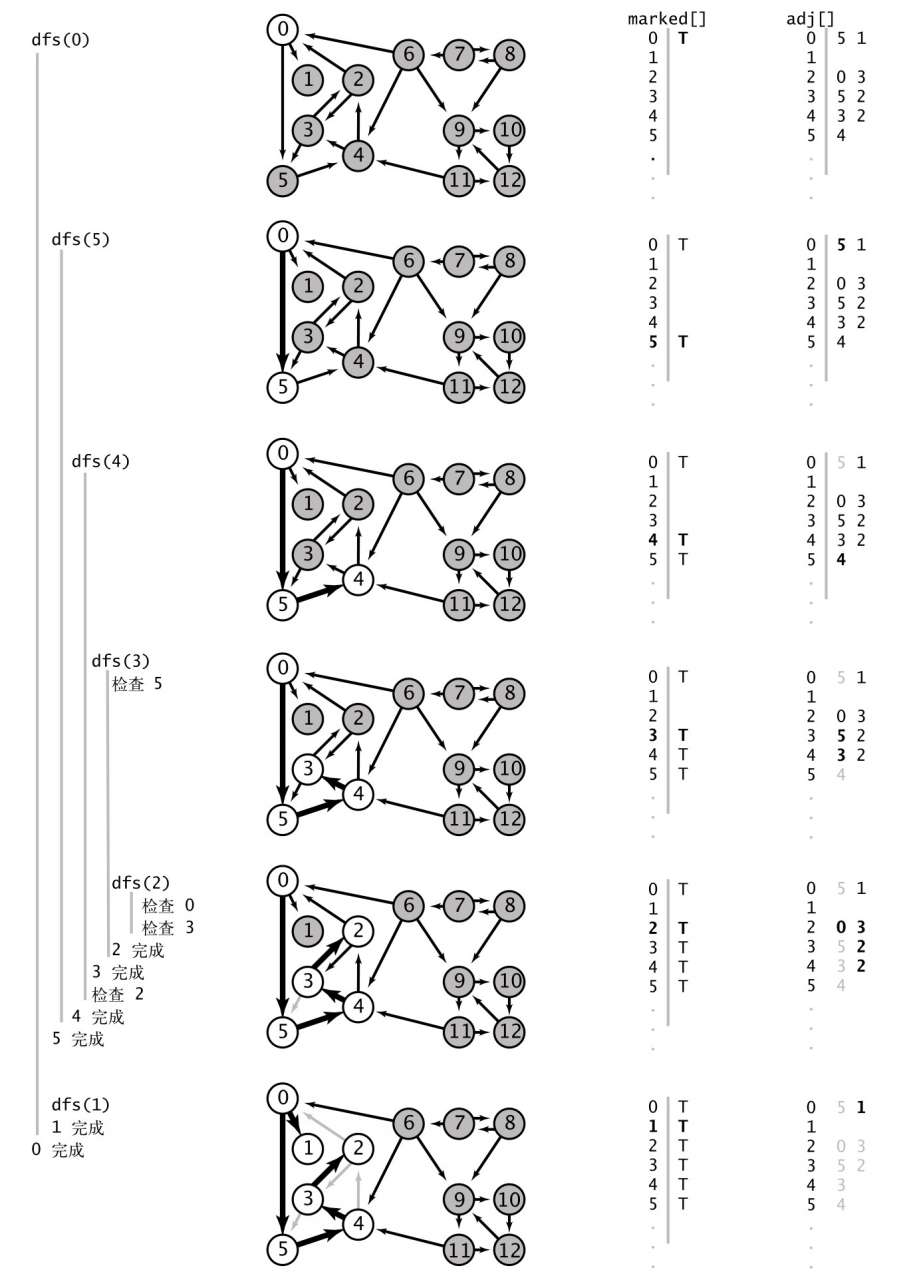
有向图的可达性（dfs）

单点可达性：一幅有向图中，起点 start 到给定顶点 v 是否存在有向路径（是否可达）

class DigraphDFS {
  private marked: Array<boolean>

  constructor(graph: Digraph, start: number) {
    this.marked = new Array<boolean>(graph.V())
    this.dfs(graph, start)
  }

  private dfs(g: Digraph, v: number) {
    this.marked[v] = true
    for (const w of g.adj(v)) {
      if (!this.marked[w]) {
        this.dfs(g, w)
      }
    }
  }

  isMarked(v: number) {
    return this.marked[v]
  }
}

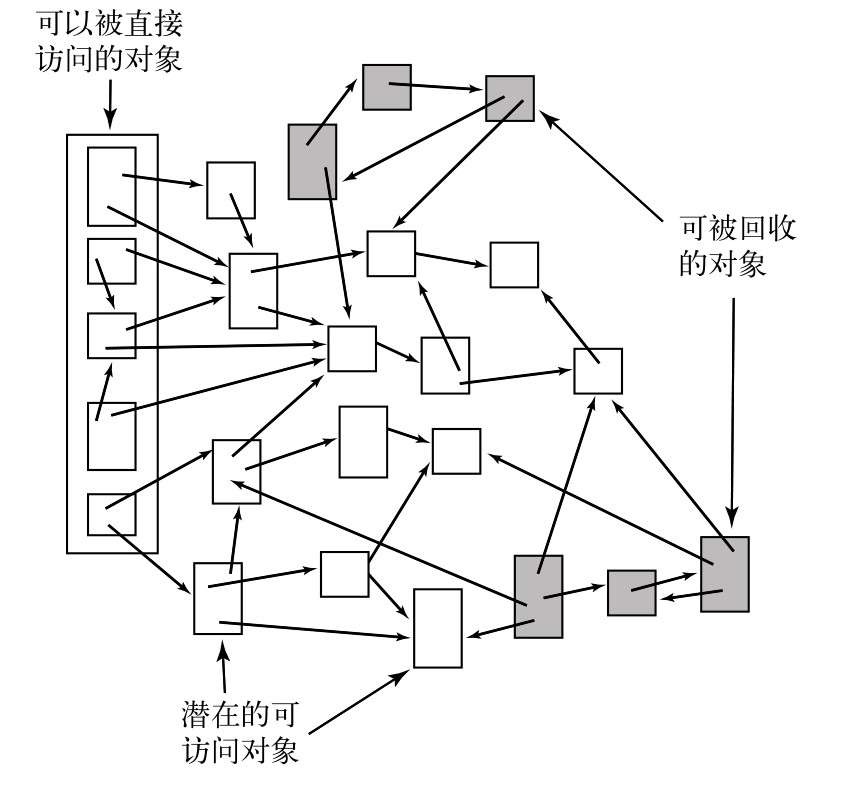
标记-清除的垃圾收集

多点可达性的应用是在内存管理当中。

标记-清除的垃圾回收策略会为每个对象保留一个位做垃圾收集之用。它会周期性地运行一个类似于 DirectedDFS 的有向图可达性算法来标记所有可以被访问到的对象，然后清理所有对象，回收没有被标记的对象，以腾出内存供新的对象使用。

有向图的寻路

• 求有向图的单点有向路径
• 求有向图的单点最短有向路径

有向图的环

在和有向图相关的实际应用中，有向环特别的重要。

任务 X 必须在任务 Y 前完成，任务 Y 必须在任务 Z 前完成，任务 Z 必须在任务 X 前完成。（x->y->z->x）

三个限制条件不能同时满足（存在环）,要检查这个错误，需要解决下面的问题：

有向环检测：给定的有向图中包含有向环吗？如果有，按照路径的方向从某个顶点并返回自己来找到环上的所有顶点。

有向无环图（DAG）：就是一幅不含有向环的有向图。

/**
 * 寻找有向环
 */
class DirectedCycle {
  private marked: boolean[]

  private edgeTo: number[]

  // 有向环的所有顶点
  private cycle: Stack<number>

  // 递归调用栈上的所有顶点
  private onStack: boolean[]

  constructor(g: Digraph) {
    this.onStack = new Array(g.V())
    this.edgeTo = new Array(g.V())
    this.marked = new Array(g.V())

    for (let v = 0; v < g.V(); v++) {
      if (!this.marked[v]) {
        this.dfs(g, v)
      }
    }
  }

  private dfs(g: Digraph, v: number) {
    this.onStack[v] = true
    this.marked[v] = true

    for (const w of g.adj(v)) {
      if (this.hasCycle()) {
        return
      }
      if (!this.marked[w]) {
        this.edgeTo[w] = v
        this.dfs(g, w)
      } else if (this.onStack[w]) {
        this.cycle = new Stack<number>()
        for (let x = v; x !== w; x = this.edgeTo[x]) {
          this.cycle.push(x)
        }
        this.cycle.push(w)
        this.cycle.push(v)
      }
    }
    this.marked[v] = false
  }

  hasCycle() {
    return this.cycle != null
  }
}

调度问题

以一个安排课程的大学生为例，有些课程是其他课程的先导课程。

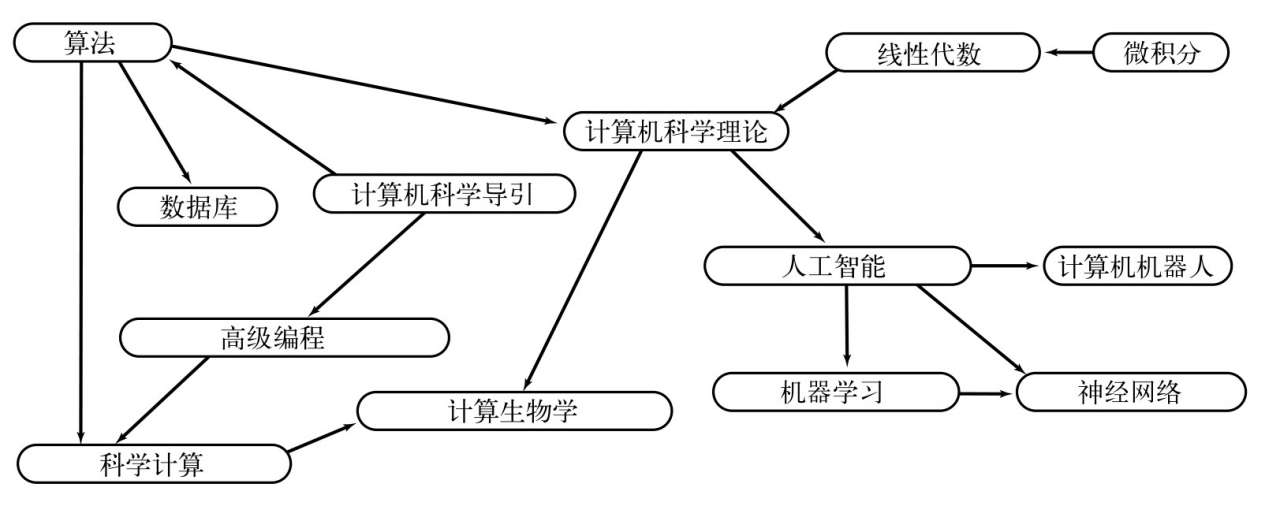
有优先级限制下的调度问题：给定一组需要完成的任务，以及一组关于任务完成的先后次序的优先级限制。在满足限制条件的前提下应该如何安排并完成所有任务？

可以画一张有向图，顶点对应任务，有向边对应任务顺序，如下图：

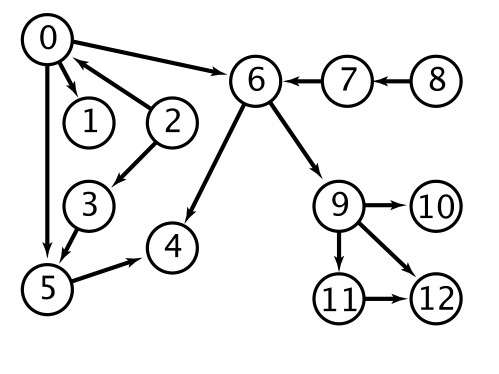
拓扑排序：给定一幅有向图，将所有的顶点排序，使得所有的有向边均从排在前面的元素指向排在后面的元素（或者说明无法做到这一点）

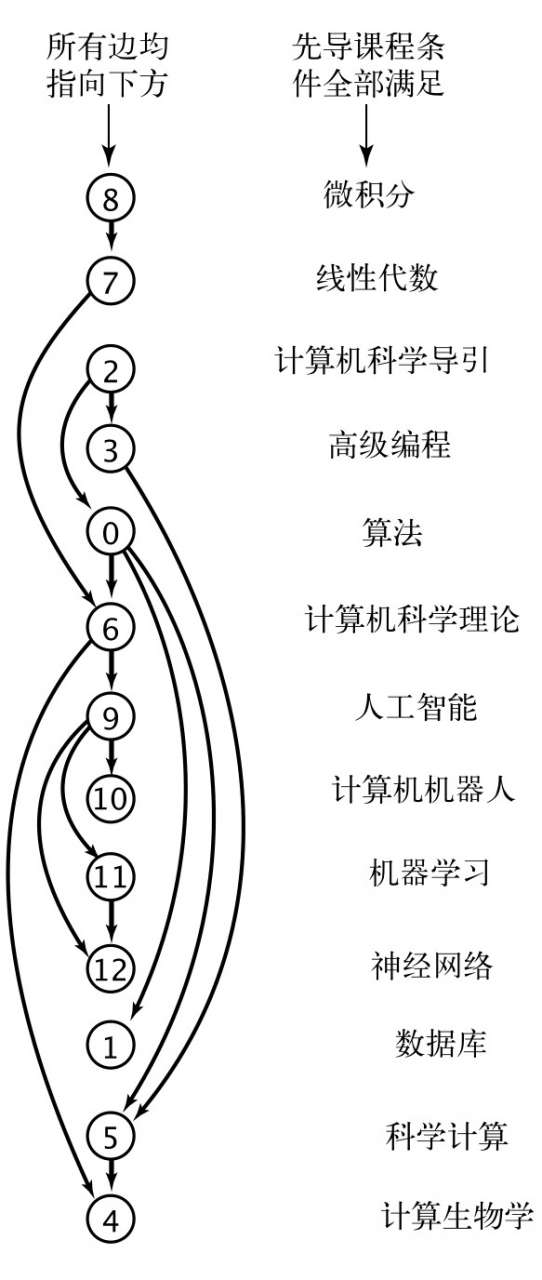
图顶点的排序：

前序：在递归调用之前将顶点加入队列。

后序：在递归调用之后将顶点加入队列。

逆后序：在递归调用之后将顶点压入栈。

当且仅当一幅有向图是无环图时它才能进行拓扑排序。

一幅有向无环图的拓扑顺序即为所有顶点的逆后序排列。

基于深度优先的顶点排序

 class DepthFirstOrder {
  private marked: boolean[]

  // 前序
  private pre: Queue<number>

  // 后序
  private post: Queue<number>

  // 逆后序
  private reversePost: Stack<number>

  constructor(g: Digraph) {
    this.marked = new Array(g.V())
    this.pre = new Queue()
    this.post = new Queue()
    this.reversePost = new Stack()
    for (let v = 0; v < g.V(); v++) {
      if (!this.marked[v]) {
        this.dfs(g, v)
      }
    }
  }

  private dfs(g: Digraph, v: number) {
    this.pre.enqueue(v)
    this.marked[v] = true

    for (const w of g.adj(v)) {
      if (!this.marked[v]) {
        this.dfs(g, w)
      }
    }
    this.post.enqueue(v)
    this.reversePost.push(v)
  }

  getPre() {
    return this.pre
  }

  getPost() {
    return this.post
  }

  getReversePost() {
    return this.reversePost
  }
}

拓扑排序

class Topological {
  private order: Iterable<number>

  constructor(g: Digraph) {
    const cycleFinder = new DirectedCycle(g)
    if (!cycleFinder.hasCycle()) {
      const dfs = new DepthFirstOrder(g)
      this.order = dfs.getReversePost()
    }
  }

  getOrder() {
    return this.order
  }
}

拓扑排序的应用：

有向图的强连通性

无向图的连通性：在无向图中如果 w-v 是连通的则既可以 w-v 也可以 v-w

有向图的可达性：在有向图中如果 w->v 是可达的，但是不一定 v->w

强连通性：有向图中两个顶点互相可达（既 w->v 又 v-> w），则称他们为强连通的。

如果一幅有向图任意两个顶点是强连通的，那么称这幅有向图也是强连通的。

性质：

自反性：任意顶点v和自己都是强连通的。

对称性：如果v和w是强连通的，那么w和v也是强连通的。

传递性：如果v和w是强连通的且w和x也是强连通的，那么v和x也是强连通的。

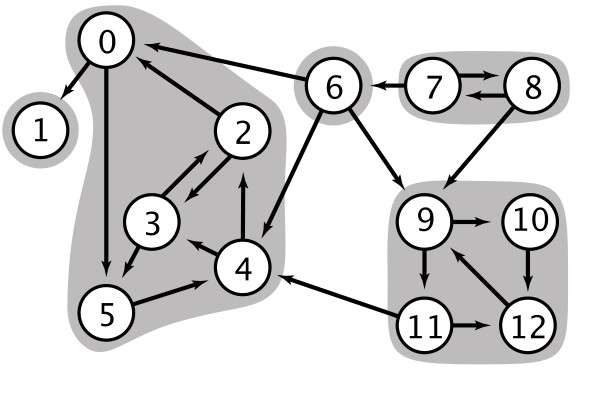
应用

计算强连通分量的 Kosaraju 算法：

public class KosarajuSCC
{
    private boolean[] marked;   // 已访问过的顶点
    private int[] id;            // 强连通分量的标识符
    private int count;           // 强连通分量的数量
    public KosarajuSCC(Digraph G)
    {
      marked = new boolean[G.V()];
      id = new int[G.V()];
      DepthFirstOrder order = new DepthFirstOrder(G.reverse());
      for (int s : order.reversePost())
          if (! marked[s])
          {  dfs(G, s); count++;  }
    }
    private void dfs(Digraph G, int v)
    {
      marked[v] = true;
      id[v] = count;
      for (int w : G.adj(v))
          if (! marked[w])
              dfs(G, w);
    }
    public boolean stronglyConnected(int v, int w)
    {  return id[v] == id[w];  }
    public int id(int v)
    {  return id[v];  }
    public int count()
    {  return count;  }
}