排序算法
| 排序算法 | 时间复杂度 | 是否基于比较 | |
|---|---|---|---|
| 冒泡、插入、选择 | O(n²) | ✅ | 适合小规模排序 |
| 快排、归并、堆排序 | O(n㏒n) | ✅ | 适合大规模排序 |
| 筒、计数、基数 | O(n) | ❌ |
冒泡排序(BubbleSort)
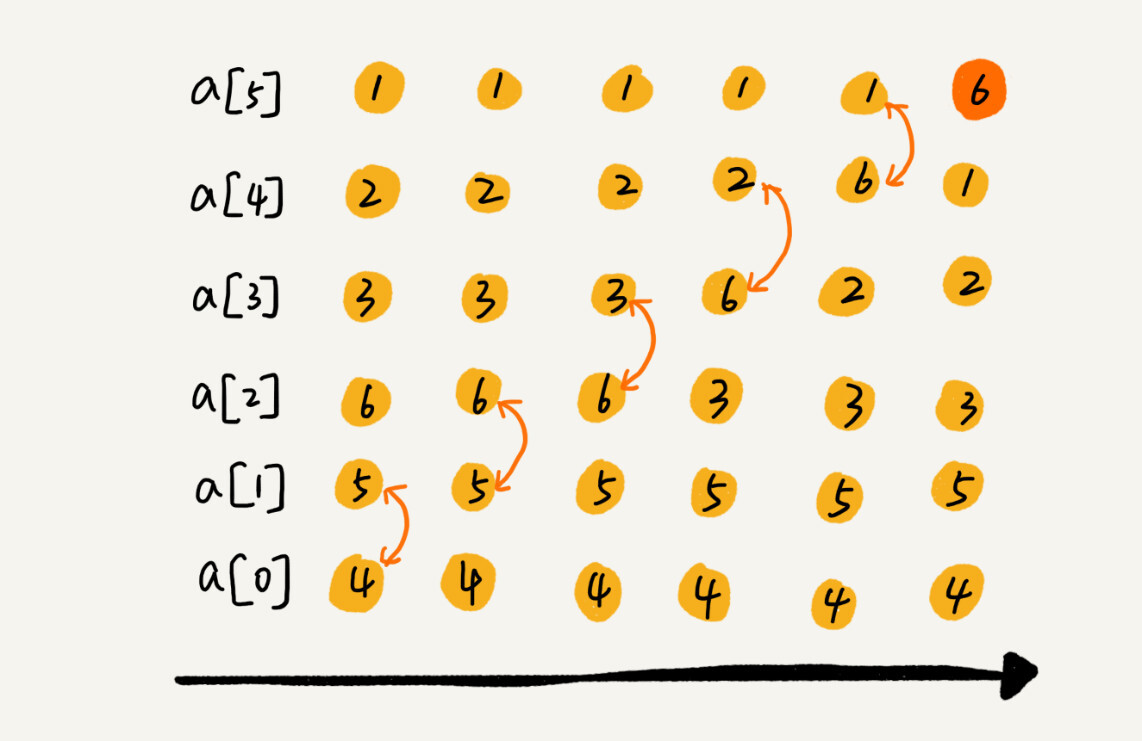
是原地排序,空间复杂度 O(1)
是稳定的排序,(判断大小相等不交换)
最好 1 次冒泡 O(n)
最坏 n 次冒泡 O(n²)
function bubbleSort (a) {
const length = a.length
for (let i = 0; i < length; i++) {
// 提前退出冒泡循环的标志位
let flag = false
// 每一次冒泡,都会把最大值排到末尾,不再参与排序,所以 length - i
for (let j = 0; j < length - i - 1; j++) {
// 交换位置
if (a[j] > a[j + 1]) {
const temp = a[j]
a[j] = a[j + 1]
a[j + 1] = temp
flag = true
}
}
if (!flag) break
}
}
插入排序(InsertionSort)

- 是原地排序,空间复杂度 O(1)
- 是稳定的排序算法
- 最好时间复杂度 O(n) 从尾到头遍历已经有序的数据
- 最坏时间复杂度 O(n²)
- 平均时间复杂度 O(n²)
/**
* 插入排序
*/
function insertionSort (a) {
// 右侧未排序区域
for (let i = 1; i < a.length; i++) {
const value = a[i]
let j = i - 1
// 左侧排序区域
for (; j >= 0; j--) {
// 向右侧移动
if (a[j] > value) {
a[j+1] = a[j]
} else {
break
}
}
// 移动完后,这个位置是空的,插入
a[j+1] = value
}
}
希尔排序(ShellSort)
希尔排序是插入排序的高效改进版
步长对应的事件复杂度
| 步长序列 | 最坏情况复杂度 |
|---|---|
 |  |
 |  |
 |  |
function shellSort(arr) {
for (let gap = arr.length >> 1; gap > 0; gap >>= 1) {
for (let i = gap; i < arr.length; i++) {
let temp = arr[i];
let j
for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap) {
arr[j + gap] = arr[j];
}
arr[j + gap] = temp;
}
}
return arr;
}
选择排序
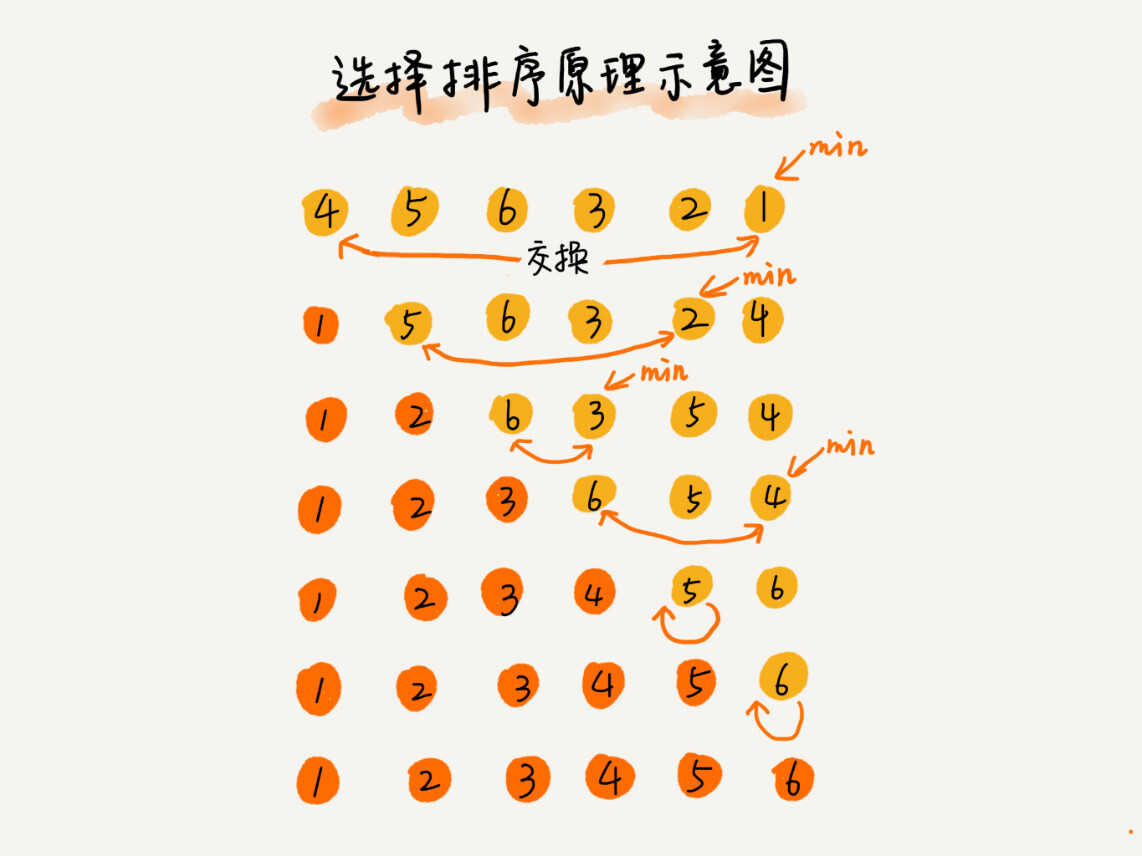
- 原地排序算法,空间复杂度 O(1)
- 最好最坏平均都是 O(n²)
- 是不稳定的排序算法
/**
* 选择排序
*/
function selectionSort (a) {
for (let i = 0; i < a.length; i++) {
let min = Number.MAX_SAFE_INTEGER
let idx = 0
for (let j = i; j < a.length; j++) {
if (a[j] < min) {
min = a[j]
idx = j
}
}
a[idx] = a[i]
a[i] = min
}
return a
}
归并排序
分治思想。大问题分解成小问题解决。
分治是一种解决问题的处理思想,递归是一种编程技巧。
思想:排序数组从中间分成前后两部分,前后分别排序再合并,就有序了
- 是稳定的排序算法
- 时间复杂度稳定,最好最坏平均都是 O(n㏒n)
- 不是原地排序,空间复杂度 O(n)
const merge = (arr, l, c, r) => {
let i = l, j = c + 1
const res = []
while (i <= c && j <= r) {
if (arr[i] <= arr[j]) {
res.push(arr[i++])
} else {
res.push(arr[j++])
}
}
while (i <= c) {
res.push(arr[i++])
}
while (j <= r) {
res.push(arr[j++])
}
for (let i = 0; i < res.length; i++) {
arr[l + i] = res[i]
}
}
const recursionMergeSort = (arr, l, r) => {
if (l >= r) return
const c = (l + r) >> 1
recursionMergeSort(arr, l, c)
recursionMergeSort(arr, c + 1, r)
merge(arr, l, c, r)
}
const mergeSort = (arr) => {
recursionMergeSort(arr, 0, arr.length - 1)
return arr
}
快速排序
思想:排序数组中下标 p 到 r 之间的一组数据,选择任意一个数据作为 pivot 分区点。小于 pivot 放左边,大于 pivot 放右边。于是就有了三个部分,再递归处理左右的数据,直到区间缩小为 1 。
快速排序的空间优化版本(原地分割),是不稳定的,需要通过牺牲性能或空间来维护稳定。
时间复杂度为 O(n㏒n) 。极端低概率情况 O(n²)
空间复杂度 O(logn) 。 logn 是快速排序调用的层数
const swap = (a, i, j) => {
const temp = a[i]
a[i] = a[j]
a[j] = temp
}
const partition = (a, l, r) => {
const pivotIndex = (l + r) >> 1
// 将 pivot 移动到末尾
swap(a, pivotIndex, r)
const pivot = a[r]
let i = l
for (let j = l; j < r; j++) {
if (a[j] <= pivot) {
swap(a, j, i)
i++
}
}
// 把 pivot 交换回去
swap(a, r, i)
return i
}
const quickSortCC = (a, l, r) => {
if (l >= r) return
const c = partition(a, l, r)
quickSortCC(a, l, c - 1)
quickSortCC(a, c + 1, r)
}
const quickSort = (a) => {
quickSortCC(a, 0, a.length - 1)
}
桶排序
需要容易的分割成 m 个桶;对数据要求苛刻,各个桶分布要求是比较均匀的。
对每个桶进行快排。
理想情况下
- 时间复杂度 时间复杂度为O(m k logk) ,(m 个桶,每个桶 k 个元素),接近O(n)
计数排序
类似于桶排序,内部不需要再快排,时间复杂度 O(n)。
基数排序
基数排序对要排序的数据是有要求的,需要可以分割出独立的“位”来比较,而且位之间有递进的关系,如果a数据的高位比b数据大,那剩下的低位就不用比较了。除此之外,每一位的数据范围不能太大,要可以用线性排序算法来排序,否则,基数排序的时间复杂度就无法做到O(n)了。