二叉堆
概念
堆(heap)
堆最初是在堆排序中提出的。(后来也被指为“垃圾回收存储区”,这里的堆数据结构不指这个)。
常见的堆有二叉堆、二项堆(binomial heap)、斐波那契堆(Fibonacci heap)。
堆是这一类数据结构的统称,一般说堆都是指二叉堆。
二叉堆(binary heap)
一般用数组表示,是一颗完全二叉树。
二叉堆常见以下两种应用:
优先队列(priority queue)
是一类抽象数据类型,优先队列中的每个元素都有各自的优先级,优先级最高的元素最先得到服务;优先级相同的元素按照其在优先队列中的顺序得到服务。优先队列往往用(二叉)堆来实现。
堆排序(heapsort)
时间复杂度为 O(nlgn)。
是一种原地排序算法。一般使用二叉堆实现。
二叉堆
二叉堆的性质
堆序性:当一棵二叉树的每个结点都大于等于(小于等于)它的两个子结点时,它被称为堆有序。
结构性:是一组能够用堆有序的完全二叉树排序的元素,并在组中按照层级储存
二叉堆有两种:最大堆(大根堆)和最小堆(小根堆)
二叉堆的实现
数据存储
一般不使用数组的第一个位置(计算会变得麻烦)
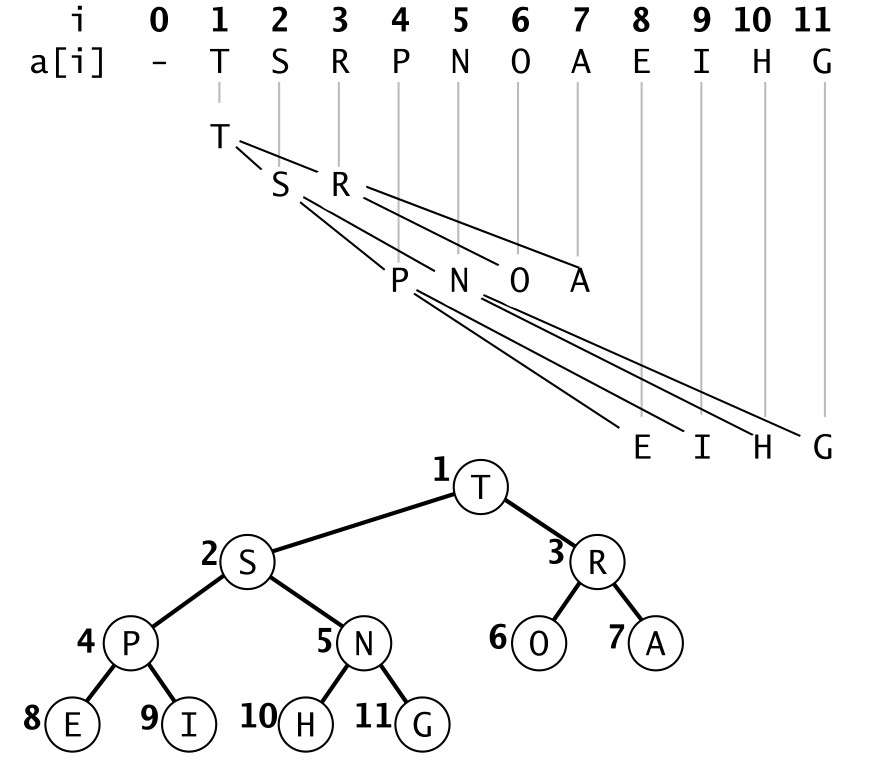
节点查找
设当前节点下标为 i
父节点:
parent = floor(i / 2)子左节点:
left = i * 2子右节点:
right = i * 2 + 1
方法定义
以最大堆的实现为例
interface MaxHeapType {
/**
* 存储数据的数组(完全二叉树)
*/
data: number[]
/**
* 数据存在 data 的 [1..N] 中,并不使用 data[0]
*/
N: number
/**
* 向堆插入一个元素
*/
insert(v: number): void
/**
* 删除堆的最大元素(堆顶)
*/
delMax(v: number): number
/**
* 返回堆中最大元素
*/
max(): void
/**
* 返回堆是否为空
*/
isEmpty(): boolean
/**
* 返回堆的元素个数
*/
size(): number
}
定义工具方法
private less(i: number, j: number) {
return this.data[i] - this.data[j] < 0
}
private swap(i: number, j: number): void {
const t = this.data[i]
this.data[i] = this.data[j]
this.data[j] = t
}
由下至上的堆有序化(上浮)的实现
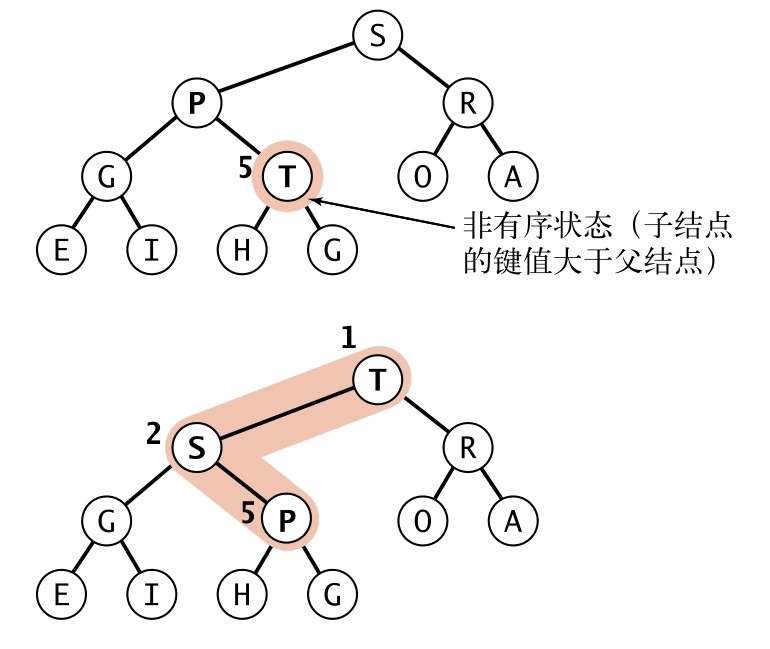
private swim(k: number) {
while (k > 1 && this.less(k >> 1, k)) {
this.swap(k >> 1, k)
k >>= 1
}
}
由上至下的堆有序化(下沉)
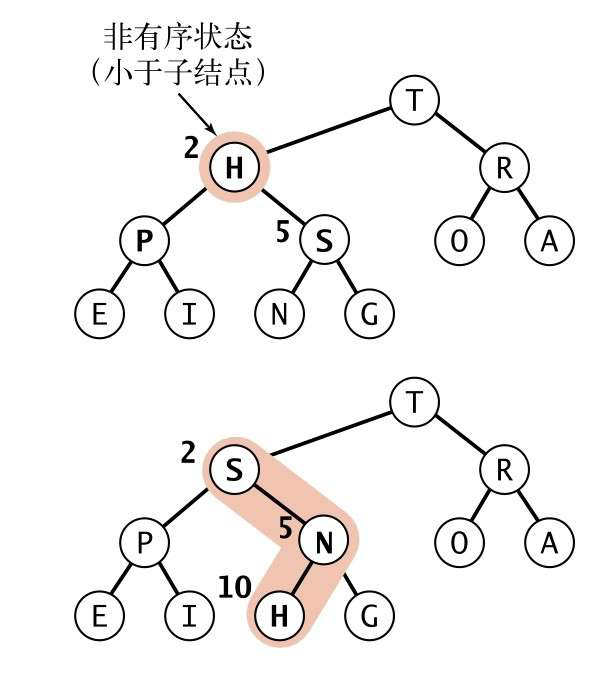
private sink(k: number) {
while (2 * k <= this.N) {
let j = 2 * k
if (j < this.N && this.less(j, j + 1)) {
j++
}
if (!this.less(k, j)) {
break
}
this.swap(k, j)
k = j
}
}
操作实现
插入操作
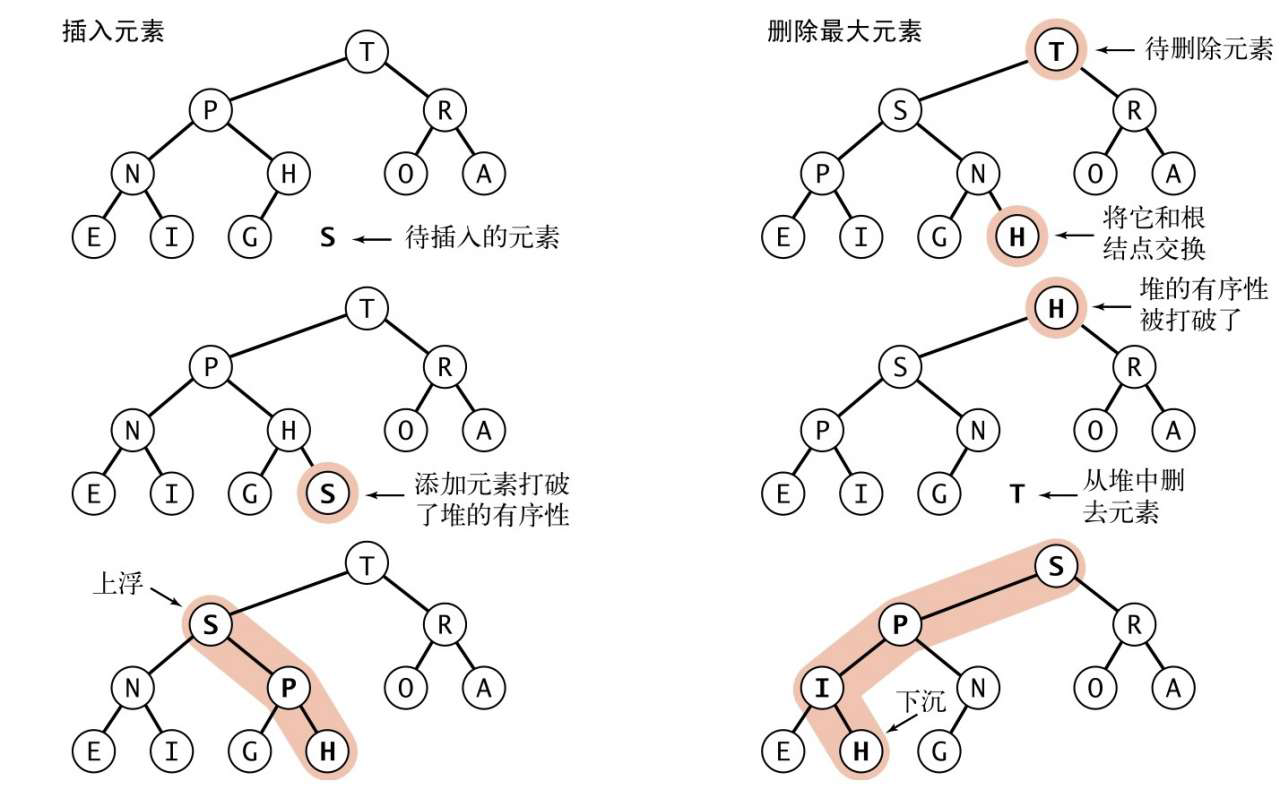
插入元素。我们将新元素加到数组末尾,增加堆的大小并让这个新元素上浮到合适的位置。
insert(v: number) {
this.data[++this.N] = v
this.swim(this.N)
}
删除操作
删除最大元素。我们从数组顶端删去最大的元素并将数组的最后一个元素放到顶端,减小堆的大小并让这个元素下沉到合适的位置。
delMax(): number {
if (this.isEmpty()) {
return null
}
const max = this.data[1]
this.swap(1, this.N--)
// 防止对象游离(避免保存一个不需要的对象引用,一些算法书的示例代码就没有这么做)
this.data[this.N + 1] = null
this.sink(1)
return max
}
以最大堆为例的实现
class MaxHeap implements MaxHeapType {
data: number[]
N: number
constructor(a: number[] = []) {
this.data = []
this.N = a.length
let i = 1
for (const n of a) {
this.data[i++] = n
}
this.buildHeap()
}
insert(v: number) {
this.data[++this.N] = v
this.swim(this.N)
}
delMax(): number {
if (this.isEmpty()) {
return null
}
const max = this.data[1]
this.swap(1, this.N--)
// 防止对象游离(避免保存一个不需要的对象引用,一些算法书的示例代码就没有这么做)
this.data[this.N + 1] = null
this.sink(1)
return max
}
max() {
return this.data[1]
}
isEmpty() {
return this.N === 0
}
size() {
return this.N
}
// 构建堆(堆化)
private buildHeap() {
for (let i = this.N >> 1; i > 0; i--) {
this.sink(i)
}
}
private less(i: number, j: number) {
return this.data[i] - this.data[j] < 0
}
private swap(i: number, j: number): void {
const t = this.data[i]
this.data[i] = this.data[j]
this.data[j] = t
}
private swim(k: number) {
while (k > 1 && this.less(k >> 1, k)) {
this.swap(k >> 1, k)
k >>= 1
}
}
private sink(k: number) {
while (2 * k <= this.N) {
let j = 2 * k
if (j < this.N && this.less(j, j + 1)) {
j++
}
if (!this.less(k, j)) {
break
}
this.swap(k, j)
k = j
}
}
}
思考
- 如何实现最小堆?
- 如何实现类似于 C++、JAVA 的
PriorityQueue
应用
- 找出第 k 大的元素
- 任务队列
参看
图片来自于算法(第四版)